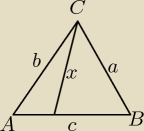
Planimetria luis: Zadanie z planimetrii. Mam dowolny trójkąt o teza : x >(a+b−c) /2 Pomoże ktoś ?

pigor: w twojej tezie chyba masz zły zwrot nierówności , bo jeśli D − punkt wspólny CD i AB i AD=y , to BD=c−y , wtedy z nierówności trójkąta dla : ΔADC i ΔBCD : x < b+y i x < a+c−y , więc dodając stronami te nierówności masz : 2x < a+b−c /:2 ⇔ x < ^a+b−c₂ . ...

luis: no i już wiem dlaczego mi nie wychodziło. Sorry ale dopiero zaczęlismy ten dział i tak nie kumałem nawet dlaczego może być coś źle. Dzięki wielkie

luis: kurde, ale to chyba a+b+ c powinno być, czy nie ? :<

pigor: ... no tak nie wiem skąd mi się wziął ten −c , przepraszam

luis: haha beka, 2 błędy w zapisie miałem, tylko tak dalej xD, jeszcz eraz thx

pigor: ... a jednak wracam tu, bo nurtowało mnie to oszacowanie z + (plusem) przy c ... kurcze , no i jest widzę, że przecież nie o takie (z góry) oszacowanie tu chodziło (jak mogłem nie zauważyć tego), dlatego podchodząc tu z .... : "innej beczki'' : b<x+y i a< x+c−y skąd po dodaniu stronami ⇒ a+b<2x+c ⇔ a+b−c<2x ⇔ ⇔ x>^a+b−c₂ i właśnie to należało udowodnić , −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− ale nie ma nic złego co nie wyjdzie na dobre , więc podsumowując mamy fajne oszacowanie z obu stron takie : ^a+b−c₂ < x < ^a+b+c₂ . ...