Zadanie z cięciwą --> bez twierdzenia o cięciwach,itp. ;) V.Abel: Mam takie pytanie, czy takie typowe zadanie, gdzie są dwie cięciwy przecinające się jednym punkcie i podane są długości 3 odcinków(mamy wyliczyć czwarty) da się zrobić BEZ twierdzenia o siecznych, cięciwach, itp.? ? ?

pigor: ... tak np. niech AB i CD− dane dwie cięciwy przecinające się w punkcie E; ł połączz końce cięciw B z C oraz A z D i otrzymujesz 2 trójkąty podobne − cecha kkk, bo ∡AOD=∡BOC − jako kąty wierzchołkowe, ∡ABC=∡ADC − jako katy wpisane oparte na tym samym łuku , stąd i ∡OCB=∡OAD − jak wyżej lub z tw. o sumie kątów w Δ, wtedy np jeśli AO=? , to masz z podobieństwa np. ^AO_OC = ^DO_BO . ...

V.Abel: dobra, racja , a jak masz na przykład podany kąt w trójkącie i dwa boki lub dwa boki i kąt (nie ważne jak rozmieszczone ) i chcesz sobie taki trójkąt rozwiązać BEZ użycia twierdzenia sinusów/cosinusów, to się da ? ? ?

pigor: ... sądzę, że da się, albo nie da się, ale to zależy od innych danych i ... tyle

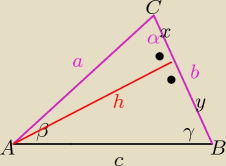Aga1.: Dane :a,b,α kolejno z funkcji trygonometrycznych obliczysz h,x, y=b−x c z twierdzenia Pitagorasa

pigor: ... oczywiście dodam, że ... miałem na myśli konkretne dane . ...

V.Abel: dzięki , pytając(retorycznie ), mając 2 sieczne, to tak jak z tymi cięciwami <?> // p.s. to wszystko i tak się w sumie sprowadza do tych twierdzeń, prawda ?

pigor: ... ano prawda, bo jednak to mocna i wbrew pozorom fajna "broń" te twierdzenia ...

Mila: Twierdzenia o siecznej i stycznej udowodniono w oparciu o podobieństwo Δ.

V.Abel: jak już pytam to jeszcze ciekawi mnie taka jedna rzecz skoro jest coś takiego jak twierdzenie sinusów i cosinusów, to jakby się tak pokusić o tangensy i ctgsy <?> Co Wy na to, jest coś takiego ? ...

pigor: ... tak, jest coś takiego i nazywa się podobnie bo tw. tangensów, a wygląda to m.in.

	a−b		tgα−β2
np. tak :		=		, ale o tym doczytaj sobie gdzieś. ...
	a+b		tgα+β2

V.Abel: super! ! ! dziękuję