wyznacz punkt C, tak aby trójkąt ABC miał najmnejszy obwód anetaa15: Dane są punkty A=(1,1) B=(6,2). Na prostej l o równaniu y−4=0, wyznacz punkt C, tak aby trójkąt ABC miał najmnejszy obwód. Z góry dziekuje za pomoc

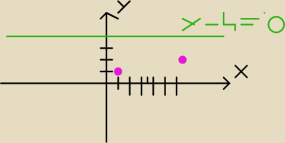
M.: prosta l jest stala( tak mi sie wydaje) zaraz pomysle dalej...

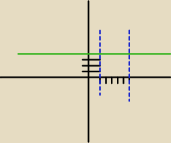
M.: punkt C musi sie zawierac gdzies tu

radek: √(1−6)²+(1−2)² + √(1−x)²+(1−4)² + √(6−x)²+(2−4)² = 0 wyjdzie prawdopodobnie rownanie kwadratowe wiec potem liczysz pierwsza wspolzedna wierzcholka paraboli ^−b_2a

radek: C(^−b_2a ; 4)

M.: o wlasnie

radek: ale azraz cos nie tak te wartosci nie beda rowne zero

radek: moment przelicze

pirate: to sie robi inaczej, liczysz odbicie punktu A wzgledem prostej i patrzysz co leży na odcinku A'B

M.: Pirate moze policzysz?

radek: nie wiem jak tych pierwiastkow sie pozbyc

radek: √26 + √x² − 2x + 10 + √x²−12x+40 = obw

M.: no wlasnie ja tez liczylam Twoim sposobem i tez na tym stanelam

radek: chyba ze x² − 2x +10 → tu liczymy pierwsza wspolzedna x² − 12x + 40 → i tu tez liczymy pierwsza wsppolzedna

radek: nie no bezsensu to nic nie da

pirate: no to masz A' (1,7) (odbicie jest dosyć proste), prosta o równaniu ax+b przechodzi przez (1,7) i (6,2), czyli masz: a+b = 7 6a + b = 2 podstawiasz wychodzi 5a = −5 czyli a=−1 co za niespodzianka! czyli b=8. Teraz liczymy przecięcie prostej y=−x+8 oraz y=4: 4 = −x + 8 x = 4 czyli jeśli niczego nie pomyliłem C = (4,4)

pirate: dowód dlaczego taki punkt daje najkrótszy obwód jest trywialny, odcinek A'B jest najkrótszą drogą między tymi punktami więc C musi znajdować się na nim

M.: a skad wiadomo ze A' to akurat jest 1,7?

pirate: no bo y=4 jest stałe więc odcinek AA' jest prostopadły do osi OY, odległość A od y=4 to 3 , odległość A' od y=4 to też 3 tylko z drugiej strony, więc A' to (1,7)

pirate: powinno być: równoległy do osi OY, prostopadły do y=4

M.: ah... dzieki za wytlumaczenie

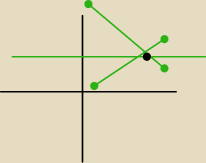
radek: pirat chodzi ci o cos takiego?

pirate: tak tylko niepotrzebnie odbiłeś sobie B, wystarczy A odbić

pirate: no i jeszcze dobrze jest napisać dlaczego odległość A'C + BC jest taka sama jak AC + BC ale to chyba oczywiste

radek: no wlasnie z uzasadnieniem mam problem bo gdyby takie cos bylo na maturze to jak mam udowodnic ze to jest akurat najkrotszy obwod sorry ale od rana ciezko mi zrozumiec

pirate: Dobra, no to patrz: Punkt C leży na prostej y=4. A' jest odbiciem A względem prostej y=4. Czyli, odległość punktu C od A' jest taka sama jak C od A. czyli możemy przyjąć, że szukamy najkrótszego AB + BA' zamiast AB + BC + CA (bo BA' to BC + CA' a jak już ustaliliśmy CA' = CA). AB mamy podane, więc tak naprawdę chodzi nam o znalezienie najkrótszego BA'. Najkrótszą drogą łączącą B i A' jest odcinek między nimi a skoro tak to C musi leżeć na nim. Jasne czy nie?

radek: jasne jak slonce haha niewpadl bym na to dzieki

anetaa15: Dziekuje BARDZO