zadanie
mikołaj: Znajdź równanie okręgu opisanego na trójkącie ABC o wierzchołkach A =(0, 0), B = (8, 0) i
C = (0, 6).
25 maj 22:27
Eta:
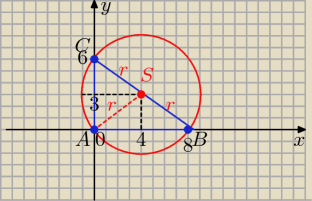
ΔABC jest prostokątny
| | 1 | |
r= |
| |BC|= ..... S −− jest środkiem odcinka BC to: S( .... , ....) |
| | 2 | |
o: (x−x
S)
2+ (y−y
S)
2= r
2
dokończ..........
25 maj 22:37
mikołaj: |BC|=10
S=4,3
(x−4)2+(y−3)2=5
25 maj 22:41
Skipper:
(x−xs)2+(y−ys)2=r2
xs2+ys2=r2
(8−xs)2+ys2=r2 ... xs2=(8−xs)2 ... 64−16xs=0 ... xs=4
ys2=(6−ys)2 ... 36−12ys=0 ... ys=3
25 maj 22:49