Jak w nierównościach modułowch ( z wartością bezwzględną ) rozpatrujemy przypadk
Sławek: Mam pytanie.
Jak w nierównościach modułowch ( z wartością bezwzględną ) rozpatrujemy przypadki różne w
zależnośći od miejsc zerowych.
I jak mamy jakiś przedział, np. , że x≤−1
i jak sprawdzam i dla −1 jest spełnione a dla −2 już nie, to mam zmienić znaki czy nie?

25 maj 17:45
Mila: Napisz konkretny przykład i zacznij rozwiązywać, to Ci wyjaśnię.
25 maj 17:47
Sławek: Dla przykładu:
|x+1| = | x−1 |
|x+1| − |x−1| = 0
i rozpatruję dla 3 przypadków:
(−∞,−1> lub (−1,1> lub (1,∞)
i jak rozpatruję 1 to dla pierwszej części nierówność |x+1| wstawię −1 to nie musze zmieniać
znaków. Ale jak już wstawię −5 to muszę.
Więc zmieniać wkoncu czy nie?

25 maj 17:49
Sławek: to jak?

Bo chciałbym zacząc nawalać przykłady a stoję w miejscu

25 maj 17:55
Sławek: pomoże ktoś?

25 maj 18:00
Sławek: Błaaaagam, ludzieeee , heeeelp

25 maj 18:12
Mila:
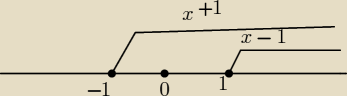
Masz przedziały: (−
∞,−1) lub <−1,1) lub <1,
∞)
1) dla x<−1
|x+1| = | x−1 | obydwa wyrażenia ujemne
−x−1=−x+1
−1=1 sprzeczność ,brak rozwiązań
2)x∊<−1,1)
x+1=−x+1
2x=0
x=0 ∊D
3) x≥1 obydwa wyrażenia dodatnie
x+1=x−1
1=−1 sprzeczność brak rozwiązań.
25 maj 18:13
Sławek: a w takim razie, wytłumacz mi proszę od czego zależy jak się wyznacza przedziały. Czy zamknięte
czy otwarte.
25 maj 18:40
Sławek: hmm?

25 maj 18:45
Sławek: Bo ja jak widać, źle określam. Mam problem z zamkniętymi a otwartymi. Niewiem od czego to w tym
przypadku zależy

25 maj 18:46
Mila:
Z defnicji wartości bezwzględnej :
|x+1|= x+1 dla x+1≥0⇔dla x≥−1
−x−1 dla x<−1
najlepiej zaznacz na osi i zapisz odpowiednio gdzie jest wartość dodatnia
25 maj 18:46
Mila: Najlepiej zrób następny przykład.sprawdzę.
25 maj 18:47
Sławek:

dalej chyba nie bardzo rozumiem...
Ja sobe to tak narysowałem:
25 maj 18:50
Mila: Będę dopiero po 22.
25 maj 18:50
Sławek: ok. to jakby mi nikt do tego czasu nie pomógł, to postaram się wyczaić Ciebie i odświeżyć wątek

To mi pomożesz ( jeżeli miałabyś ochotę

)
25 maj 18:52
Mila: Wpadłam na 10 minut.
Zauważ, że w przedziale (−∞,−1) obydwa wyrażenia : (x+1) i(x−1) są ujemne, a wartość bewzględna
jest nieujemna zatem zmieniasz znak w obydwu wyrażeniach;
−x−1 i −x+1. ( i tak np dla −5 mamy −(−5)−1=5−1=4 a drugie −(−5)+1=5+1=6 widzisz, wynik
dodatni!)
Masz rozwiązać równanie |x+1| = | x−1|
wtedy w tym przedziale równanie bez wznaku wartości bezwzględnej ma postać:
−x−1=−x+1
stąd −1=1 sprzeczność, brak rozwiązania.
No pomyśl dalej.
25 maj 20:22
Sławek: tak rozumiem

Ale mi chodzi o to, czemu bierzesz takie przedziały a nie inne

Czemu (−∞,−1) a nie (−∞,−1>
Czy jest jakaś reguła na to kiedy domknięty a kiedy nie? Bo wiem, że to tak sobie mogę w głowie
posprawdzać i wyznaczę dobrze, ale to troche kłopotliwe

25 maj 20:37
Mila: x+1<0 dla x<−1 a dla x=−1 ma wartość 0 więc nie trzeba zmieniać znaku.
25 maj 22:07
Sławek: ehh, nie kumam ..
25 maj 22:10
Sławek: Może bys mi chciała to jeszcze raz wyłożyć... ale tak dosłownie kroczek po kroczku, jak dla
amatora totalnego
25 maj 22:15
Mila: No to czytaj definicję :
Z definicji wartości bezwzględnej :
|x+1|= x+1 dla x+1≥0⇔dla x≥−1
oraz −x−1 dla x<−1
to przecież narzuca Ci przedział <−1,∞) dla postaci x+1
oraz (−∞,−1) dla postaci −x−1
konkret |−5|=−(−5)=5
|5|=5
25 maj 22:17
krystek: Np. Ix−2I=5
I przypadek dla x≥2 masz x−2=5
II przypadek dla x<2masz −(x−2)=5
25 maj 22:19
Sławek: a np. w tym przykładzie:
|x+1|+2|x−1| = 5 ?
25 maj 22:21
Sławek: to co mi Mila wytłumaczyłaś kumam

Ale to jest tylko dla |x+1| ale jeszcze jest |x−1|
25 maj 22:27
Sławek: i wtedy będe miał 4 przedziały..
25 maj 22:27
Mila: x+1≥0⇔x≥−1
x−1≥0⇔x≥1 i masz 3 przedziały.
Twój przykład
|x+1|+2|x−1| = 5 ?
1) x∊(−∞,−1) obydwa wyrażenia ujemne (zmieniam znaki)
−x−1+2(−x+1)=5
rozwiązuj dalej
25 maj 22:34
Mila: Krystek, Witam Cię ciepło.
25 maj 22:34


 Bo chciałbym zacząc nawalać przykłady a stoję w miejscu
Bo chciałbym zacząc nawalać przykłady a stoję w miejscu


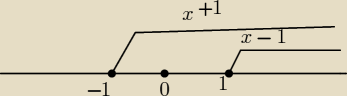 Masz przedziały: (−∞,−1) lub <−1,1) lub <1,∞)
1) dla x<−1
|x+1| = | x−1 | obydwa wyrażenia ujemne
−x−1=−x+1
−1=1 sprzeczność ,brak rozwiązań
2)x∊<−1,1)
x+1=−x+1
2x=0
x=0 ∊D
3) x≥1 obydwa wyrażenia dodatnie
x+1=x−1
1=−1 sprzeczność brak rozwiązań.
Masz przedziały: (−∞,−1) lub <−1,1) lub <1,∞)
1) dla x<−1
|x+1| = | x−1 | obydwa wyrażenia ujemne
−x−1=−x+1
−1=1 sprzeczność ,brak rozwiązań
2)x∊<−1,1)
x+1=−x+1
2x=0
x=0 ∊D
3) x≥1 obydwa wyrażenia dodatnie
x+1=x−1
1=−1 sprzeczność brak rozwiązań.


 dalej chyba nie bardzo rozumiem...
Ja sobe to tak narysowałem:
dalej chyba nie bardzo rozumiem...
Ja sobe to tak narysowałem:
 To mi pomożesz ( jeżeli miałabyś ochotę
To mi pomożesz ( jeżeli miałabyś ochotę  )
)
 Ale mi chodzi o to, czemu bierzesz takie przedziały a nie inne
Ale mi chodzi o to, czemu bierzesz takie przedziały a nie inne  Czemu (−∞,−1) a nie (−∞,−1>
Czy jest jakaś reguła na to kiedy domknięty a kiedy nie? Bo wiem, że to tak sobie mogę w głowie
posprawdzać i wyznaczę dobrze, ale to troche kłopotliwe
Czemu (−∞,−1) a nie (−∞,−1>
Czy jest jakaś reguła na to kiedy domknięty a kiedy nie? Bo wiem, że to tak sobie mogę w głowie
posprawdzać i wyznaczę dobrze, ale to troche kłopotliwe 
 Ale to jest tylko dla |x+1| ale jeszcze jest |x−1|
Ale to jest tylko dla |x+1| ale jeszcze jest |x−1|