w trójkącie ABC o bokach długości |AB|=10 , |BC|= 8 i |AC|= 6 poprowadzono prost
;/: Proszę o pomoc
w trójkącie ABC o bokach długości |AB|=10 , |BC|= 8 i |AC|= 6 poprowadzono prosta DE równoległa
do boku AC. oblicz długości odcinków DB i EB, jesli prosta ED podzieliła:
a) obwód trójkąta ABC na dwie równe części
b) trójkąt ABC na dwie figury o równych polach
24 maj 21:43
123:
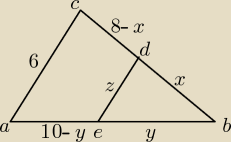
a)
| 6 + 8 + 10 | | 24 | |
| = x + y ⇒ x + y = |
| ⇒ x + y = 12 ⇒ x = 12 − y |
| 2 | | 2 | |
10(12 − y) = 8y
120 − 10y = 8y
18y = 120
| | 20 | | 36 − 20 | | 16 | |
x = 12 − |
| ⇒ x = |
| ⇒ x = |
| |
| | 3 | | 3 | | 3 | |
24 maj 22:04
zaneta: dziękuje

24 maj 22:07
123: b)
p
1 − połowa obwodu dużego trójkąta
p
2 − połowa obwodu małego trójkąta
P
1 − pole dużego trójkąta
P
2 − pole małego trójkąta
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
p
1 = 12
P
1 =
√(p1 − 10)(p1 − 8)(p1 − 6)
P
1 =
√(12− 10)(12 − 8)(12 − 6)
P
1 =
√2*4*6
P
1 =
√48
P
1 = 4
√3
P
2 =
√(p2 − z)(p2 − x)(p2 − y)
| | z + x + y | | z + x + y | | z + x + y | |
P2 = √( |
| − z)( |
| − x)( |
| − y) |
| | 2 | | 2 | | 2 | |
| | −z + x + y | | z − x + y | | z + x − y | |
P2 = √( |
| )( |
| )( |
| ) |
| | 2 | | 2 | | 2 | |
| x | | 8 | | 6x | |
| = |
| ⇒ 8z = 6x ⇒ z = |
| |
| z | | 6 | | 8 | |
| 8 | | 10 | | 10x | |
| = |
| ⇒ 10x = 8y ⇒ y = |
| |
| x | | y | | 8 | |
P
1 = P
2
| | −6x8 + x + 10x8 | | 6x8 − x + 10x8 | |
4√3 = √( |
| )*( |
| ) |
| | 2 | | 2 | |
| | (−6x + 8x + 10x)(6x − 8x + 10x)(6x + 8x − 10x)83 | |
48 = |
| |
| | 8 | |
| | (−6x + 8x + 10x)(6x − 8x + 10x)(6x + 8x − 10x) | |
48 = |
| |
| | 82 | |
3072 = 12x*8x*4x
3072 = 384x
3
x
3 = 8
x = 2
| | 10*4 | | 40 | |
y = |
| ⇒ y = |
| ⇒ y = 5 |
| | 8 | | 8 | |
24 maj 22:44
123: I nikt mi za to nie płaci... Mam nadzieję, że przynajmniej pomogłem

24 maj 22:44
labi7: zle
11 mar 18:55
yolo: Jak w końcu policzyć ten b) głowie sie ale nie daje rady −.−
18 kwi 19:05
moralizator: z jakiego wzoru wzięła się pierwsza linijka z podpunktu a)?
25 lut 16:45
moralizator: Proszę o pomoc
25 lut 17:06
Mania: Dlaczego połowa obwodu to x+y?
25 lut 20:24
Mania: Dobra, nie było pytania

25 lut 20:25
Mania: moralizator, z danych z zadania; pierwsza część to połowa obwodu, a druga to druga połowa
figury, czyli nasze szukane x i y

25 lut 20:28
prosta: b)
| P2 | | 0,5xysinα | | xy | | xy | | 1 | |
| = |
| = |
| ⇔ |
| = |
| ⇔xy=40 |
| P1 | | 0,5*8*10 *sinα | | 80 | | 80 | | 2 | |
25 lut 20:47
janush: Skąd wiadomo, że pole trójkąta BDE jest równe połowie pola trójkąta ABC?
19 sty 15:57
Mila:
Z treści zadania punkt (b)
19 sty 20:43
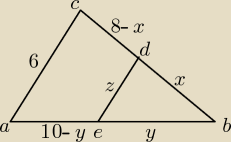 a)
a)



