obliczanie wysokosci trapezu Życie matematyka jest ciężkie: potrzebuje pomocy w rozwiązaniu takiego zadania: dany jest trapez, w którym podstawy mają długość a=11 i b=9 oraz ramiona tworzą z dłuższą podstawą kąty o miarach α=60 i β=30. Obliczyć wysokość trapezu oraz długośc ramienia trapezu c przylegającego do kąta α. Nie mam pojęcia jak to ugryźć, będę wdzięczny za pomoc

pytający:

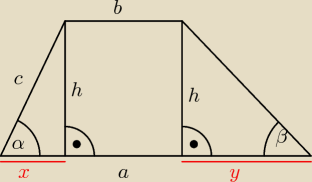
⎧	a,b,c,h,x,y >0
⎜	x+y=a−b ⇒ x+y=2
⎨	tgβ=h/y ⇒ h=y*tgβ
⎩	tgα=h/x ⇒ h=x*tgα

⎧	y*tg30o=x*tg60o
⎩	x+y=2 ⇒ x=2−y

y*tg30^o=(2−y)*tg60 ⇒ y=3/2 ⇒ x=1/2

	√3
h=x*tg60o=1/2*√3=
	2

c²=x²+h²

	1		√3
c2=(		)2+(		)2
	2		2

	1		3
c2=		+
	4		4

c²=1 c=1

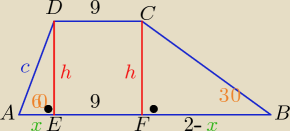
Eta: |AB|= 12 , |AE|=x |FB|= 2−x , x€ (0,2) bo: |AB|= x+9+2−x= 12

h		h		√3
	=tg60o ⇒ h= √3*x i		= tg30o ⇒ h=		*(2−x)
x		2−x		3

	√3		1
√3*x=		(2−x) ⇒ 4x=2 ⇒ x=
	3		2

	√3
to: h= √3*x =
	2

c=2x= 1

Marti: z własności kąta α=60 to by winikalo ze c=2x ...