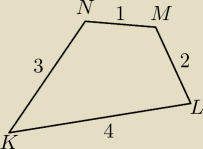
 W czworokącie KLMN na dołączonym rysunku kąt LMN ma miarę 120 stopni. Oblicz pole tego
czworokąta.
Utknęłam na tym zadaniu, byłabym Wam wdzięczna za pomoc
W czworokącie KLMN na dołączonym rysunku kąt LMN ma miarę 120 stopni. Oblicz pole tego
czworokąta.
Utknęłam na tym zadaniu, byłabym Wam wdzięczna za pomoc 
| 1 | ||
PΔNML= | *1*2*sin120 | |
| 2 |
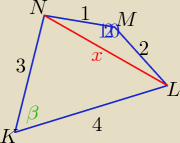 P= P(ΔNML) +P(ΔKLN)
P= P(ΔNML) +P(ΔKLN)
| 1 | √3 | |||
P(ΔNML)= | *2*1*sin120o = sin60o= | |||
| 2 | 2 |
| 1 | ||
x2=12+22−2*1*2*cos120o= 5+2= 7 cos120o= −cos60o= − | ||
| 2 |
| 42+32 −7 | 3 | |||
cosβ= | = | |||
| 2*4*3 | 4 |
| 9 | √7 | |||
sinβ= √1− | = | |||
| 16 | 4 |
| 1 | ||
P(ΔKLN)= | *4*3*sinβ=..... | |
| 2 |
