pytanie tn: Kiedy ciąg jest ograniczony?

Trivial: A jak myślisz?

tn: że ma granicę?

tn: O Trivial możemy przez jakieś 10min pogadać o ciągach?

Trivial: ok. Za 10 min, przez 10 min.

tn: ok, powiedz kiedy będziesz gotów!

Trivial: ok.

tn: ja będę za 5 min, poczekasz, czy czas stracę ?

Trivial: spoko mam cały wolny wieczór.

tn: co oznacza, że ciąg jest ograniczony?

Trivial: To znaczy, że wszystkie wyrazy tego ciągu od pewnego n₀ są ograniczone przez liczbę

Trivial: A, nie sorry. Wszystkie wyrazy są ograniczone przez tę liczbę. Pomyliło mi się.

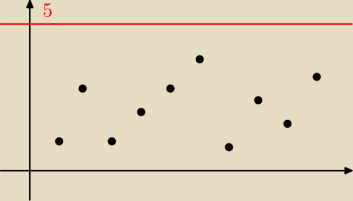
Trivial: Proszę bardzo, przykład. Ciąg ograniczony od góry przez 5.

Mila:

	nπ		nπ
an=sin		ciąg ograniczony |sin		|≤1
	2		2

a_n=(−1)ⁿ ciąg ograniczony

tn: czyli nie przekroczą jakiejś liczby?

Trivial: Tak. Np. ciąg a_n = (−1)ⁿ jest ograniczony od góry przez 2, 3, π, e, ... Jeżeli ciąg jest ograniczony zarówno od góry jak i od dołu, to mówimy że jest ograniczony. Czyli a_n = (−1)ⁿ − ograniczony od dołu np. przez −2. Zatem (−1)ⁿ to ciąg ograniczony.

tn: Ok, ale piątka niekoniecznie będzie granicą, gdyż elementy się nie zbliżają stopniowo coraz bliżej?

Trivial: Tak. Równie dobrze mogłaby być to szóstka. Jeżeli można ograniczyć od góry przez jakąkolwiek liczbę, to ciąg jest wtedy 'ograniczony od góry'. Analogicznie od dołu. Jeżeli jest jednocześnie ograniczony od góry i od dołu, to wtedy jest 'ograniczony'.

tn: ok, a jeśli istnieje granica jakakolwiek − ciąg do niej zbiega, to ciąg jest ograniczony?

Trivial: Tak. Jest wtedy ograniczony. Nie wiemy przez jaką liczbę, ale jest.

tn: Ok, powiedz mi jeszcze jak wygląda definicji ciągu rozbieżnego?

Trivial: CIąg jest rozbieżny do nieskończoności, jeżeli dla każdego, dowolnie dużego M, wszystkie wyrazy od pewnego n₀ są od niego większe. lim a_n = +∞ :⇔ ∀M∊R ∃n₀∊N : ∀n>n₀ |a_n| < M.

Trivial: |a_n| > M.

tn: aha, czyli gdy one będą dążyć do nieskończoności ?

tn: dodatniej bądź też ujemnej?

Trivial: Tak. To definicja dla +∞. Dla −∞ analogicznie, tylko w drugą stronę nierówność: |a_n| < M.

tn: czyli jest to jak gdyby odwrotność definicji ciągu zbieżnego?

Trivial: Nie wiem. Po prostu taka definicja.

tn: Więc jeśli rozwiążę tą nierównosć to okaże sie, od jakiego momentu te wyrazy są rozbieżne do nieskończoności?

tn: tylko czy tam na pewno ma być wartość bezwzględna?

Trivial: Tak, masz rację. Powinno być: lim a_n = ∞ :⇔ ∀M∊R ∃n₀∊N : ∀n>n₀ |a_n| > M. lim a_n = +∞ :⇔ ∀M∊R ∃n₀∊N : ∀n>n₀ a_n > M. lim a_n = −∞ :⇔ ∀M∊R ∃n₀∊N : ∀n>n₀ a_n < M. A ja lepiej pójdę spać, bo już nie myślę. Na razie.

tn: dzięki i tak już wszystko rozumię

Trivial: Powodzenia.

abc: [ C_W ] = ^J_kg*K