Udowodnij, ze pole wielokata o n bokach. lmazurek18: Udowodnij że pole wielokata o n bokach opisanego na okręgu wyraża się wzorem: P=p*r, gdzie p−połowa obwodu wielokata, n− promien okręgu wpisanego w ten wielokat.

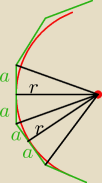
Artur z miasta Neptuna: Dla wielokąta foremnego.

	j
wielokąt taki jest złożony z 2*n trójkątów prostokątnych o bokach a i r (a =		; gdzie j =
	2

długość boku, r = promień okręgu) tak więc:

	j   * r 2		n*j * r		n*j
Pw = 2*n *		=		= p*r .... ponieważ		= Obww
	2		2		2

Dla dowolnego wielokąta nie ma równych boków, ale procedura wygląda podobnie −−− promień kierujesz do środka odcinka (jest prostopadły do boku), tworzone są dwa trójkąty prostokątne ... i tak z każdym bokiem

lmazurek18: Kurcze, jak dasz radę to zrób to ...

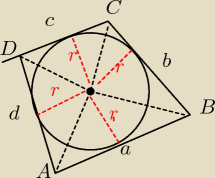
Mila: Promienie są prostopadłe do boków w punkcie styczności ( są zatem wysokościami Δ)

	1		1		1		1
Pwielokąta=		*a*r+		*b*+r		*c*r+		*d*r=
	2		2		2		2

1		1
	*r*(a+b+c+d)=p*r gdzie p=		(a+b+c+d)
2		2