Planimetria. Wielokąt foremny. Promień okręgu wpisanego
V.Abel: Oblicz promień okręgu wpisanego w ośmiokąt foremny.
Moja metoda, to pole deltoidu= pole 2 sąsiadujących trójkątów, ale nie wychodzi, co Wy na
to..(?)
22 maj 22:11
Mila: 1) bok jest dany?
2) znasz funkcje trygonometryczne?
22 maj 23:00
V.Abel: nie jest dany żaden bok, po prostu masz wyznaczyć taki ogólny wzór...
czy wiesz może jak to zrobić . funkcje znam, ale podpowiedz " co do czego i gdzie ", proszę...
23 maj 21:08
Beti: a jaka jest odpowiedź do tego zadania?
23 maj 21:31
Maslanek:
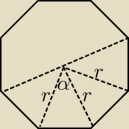
| | 180−45 | | 135 | |
Zatem kąty przy podstawie są równe |
| = |
| . |
| | 2 | | 2 | |
Z twierdzenia cosinusów:
| | 135 | |
Stąd r2 = U{a2}{2−2cos |
| . |
| | 2 | |
23 maj 21:36
Maslanek: Ewentualnie z twierdzenia sinusów:
23 maj 21:37
Maslanek: Wyżej popełniłem błąd rzeczowy

Nie ten kąt wziąłem w twierdzeniu cosinusów. Oczywiście cos45

23 maj 21:38
Beti: Maslanek ale okrąg ma być wpisany w ośmiokąt. Oznacza to, że r będzie wysokością
trójkącików, a nie jego ramieniem.
23 maj 21:39
Maslanek: No tak...

23 maj 21:41
Maslanek:
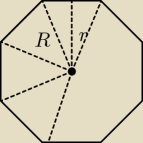
No dobra.

| | 135 | | r | |
Ale to mając R z funkcji trygnometrycznych: sin |
| = |
| . |
| | 2 | | R | |
| | 135 | |
Z tego r= R*sin |
| . To już by dawało jakiś wynik  |
| | 2 | |
23 maj 21:44
Maslanek: Idę wybrać fragment na polski

Baju

23 maj 21:46
Mila:
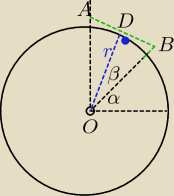
α=45
0
β=22,5
0 , ctg22,5
0=
√2+1 jest w tablicach, (wiele razy na forum liczone)
W ΔAOB:
|AB|=a
OD=r jest wysokością , dzieli kąt na połowy
W ΔBDO:
r=0,5a*ctg22,5
0=0,5*a*(
√2+1)
albo w takiej postaci:
| | a(√2+1) | |
r= |
| promień okręgu wpisanego w ośmiokąt foremny o boku a |
| | 2 | |
23 maj 22:39
V.Abel: Dziękuję wszystkim za zaangażowanie i pomoc

.
Próbowałem z deltoidu, ale tam przecież nie jestem w stanie wyliczyć h=r.
Dzięki

Pzdr.
24 maj 21:47
Maslanek: | | a√2 | |
Dlaczego u mnie wychodzi r= |
| ? |
| | 2 | |
24 maj 21:52
V.Abel: mi się podoba sposób Mili

, wzięła ctg kąta 22,5, co Ty na to. Z moich obserwacji wziąłeś kąt
135/2= 75, to nie to samo. ?...
24 maj 21:54
Maslanek: Ale u mnie sinusy się skracają. Ich zwyczajnie nie ma...

24 maj 21:55
V.Abel: to jak Ci wyszło takie r ?

właściwie to jak Ty się pozbyłeś tego R

?

24 maj 21:58
Maslanek: To R to r z dwóch postów wcześniej

. Był obliczony promień opisanego okręgu.
no, a r = R*sinβ
24 maj 22:00
Kacper:
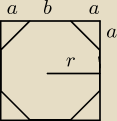
b=2 <=> a =
√2
całość (b+2a) = 2 +2
√2
r= 1/2(b+2a) = 1+
√2
24 lut 17:47

 Nie ten kąt wziąłem w twierdzeniu cosinusów. Oczywiście cos45
Nie ten kąt wziąłem w twierdzeniu cosinusów. Oczywiście cos45


 No dobra.
No dobra. 

 Baju
Baju 
 α=450
β=22,50 , ctg22,50=√2+1 jest w tablicach, (wiele razy na forum liczone)
W ΔAOB:
|AB|=a
OD=r jest wysokością , dzieli kąt na połowy
W ΔBDO:
α=450
β=22,50 , ctg22,50=√2+1 jest w tablicach, (wiele razy na forum liczone)
W ΔAOB:
|AB|=a
OD=r jest wysokością , dzieli kąt na połowy
W ΔBDO:
 .
Próbowałem z deltoidu, ale tam przecież nie jestem w stanie wyliczyć h=r.
Dzięki
.
Próbowałem z deltoidu, ale tam przecież nie jestem w stanie wyliczyć h=r.
Dzięki  Pzdr.
Pzdr.
 , wzięła ctg kąta 22,5, co Ty na to. Z moich obserwacji wziąłeś kąt
135/2= 75, to nie to samo. ?...
, wzięła ctg kąta 22,5, co Ty na to. Z moich obserwacji wziąłeś kąt
135/2= 75, to nie to samo. ?...

 właściwie to jak Ty się pozbyłeś tego R
właściwie to jak Ty się pozbyłeś tego R  ?
? 
 . Był obliczony promień opisanego okręgu.
no, a r = R*sinβ
. Był obliczony promień opisanego okręgu.
no, a r = R*sinβ
 b=2 <=> a = √2
całość (b+2a) = 2 +2√2
r= 1/2(b+2a) = 1+√2
b=2 <=> a = √2
całość (b+2a) = 2 +2√2
r= 1/2(b+2a) = 1+√2