pilne, zadanie tekstowe z kwadratem mixek: w kwadracie o boku długości 12cm poprowadzono dwie proste równoległe do jednej z przekątnych kwadratu w równych do niej odległościach. proste te podzieliły kwadrat na trzy figury o równych polach oblicz odległość tych prostych. proszę o szybką odpowiedz

Basia: a+b=12

	a*a		a2
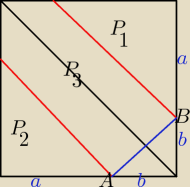
P1 =P2 =		=
	2		2

	a2
P3 = 144 − 2*		= 144 − a2
	2

stąd wynika, że

	a2
144 − a2 =		/*2
	2

144*2 − 2a² = a² 288 − 3a² = 0 3(96−a²) = 0 96−a²=0 a = √96 = √4*24 = 2√4*6 = 4√6 czyli b = 12−4√6 = 4(3−√6) szukane jest d z tw. Pitagorasa d² = 2b² = 16(3−√6)² dalej już sobie policz

mixek: czy dobrze mi wyszło że d=4√30−12√6

Basia: opuściłam 2 d² = 2*16(9 − 6√6+6) = 32(15−6√6) = 96(5−2√6) d = √96(5−2√6) = 4√6(5−2√6) taki sam wynik jak Twój, ale policzmy dalej (5−2√6) = (a−b√6)² = a²+6b² − 2ab√6 ab = 1 a²+6b² = 5

1
	+6b2 − 5 = 0
b2

1 + 6b⁴ − 5b² = 0 6b⁴−5b²+1 = 0 Δ = 25−24 = 1

	5−1		4		1
b2 =		=		=
	12		12		3

lub

	5+1		1
b2 =		=
	12		2

biorę sobie drugi wynik bo mi się bardziej podoba (ale mogę i pierwszy)

	1
b =
	√2

a = √2 5 − 2√6 = (√2 − U{√6}{√2)² = (√2−√3)² i wtedy mamy d = 4√6(√2−√3)² = 4√6*|√2−√3| = 4√6*(√3−√2) chyba trochę ładniej wygląda

Piotr: πγΔπ∞≥≤