[Z[dpelczar - zadania]]
dpelczar: Tu wklejajcie fajne zadania maturalne dla mnie − poziom rozszerzony
W razie potrzeby liczę na waszą pomoc − z góry dziekuje 
26 kwi 18:10
tim: Jaki dział głównie cie interesuje?
26 kwi 18:12
26 kwi 18:17
dpelczar: najgorzej u mnie z prawdopodobieńtwem... wiec sam sie go poucze...
Po protu takie zadanka jak na maturze będą:
logarytmy, wart. bezwzględna, wielomiany, trygonometria (jak mam dobry dizen to mi
idzie), rownania i nierownosci z parametrem... itp...
26 kwi 18:21
tim: Z parametrem [z matury] masz radka

to jest maturalne.
26 kwi 18:22
tim: Zadanie powiedzmy za 3 punkty

mx
2 − 3(m + 1)x + m = 0
Dla jakich m równanie nie ma rozwiązań w zbiorze rzeczywistych

26 kwi 18:24
radek: czyli Δ<0 Δ= [−3(m+1)]2 − 4m2 < 0
26 kwi 18:26
tim: To dla dppelczara chyba

26 kwi 18:26
tim: Wg mnie najlepszym rozw. bedzie rozw. zadan na forum.

26 kwi 18:32
dpelczar: wiec zadanie od timusia

licze delte i wychodzi 5m
2 + 6m +1 < 0 (bo wtedy nie ma rozwiązań = miejsc zerowych)
5m
2 + 6m +1 < 0
(m + 1)( m +
15) < 0
m= −1 m=−
15
równanie nie ma rozwiazania dla m ∈ (−1 ;
15)
zgadza sie

26 kwi 18:40
tim: Przykro mi

Metoda ok, ale gorzej z rozwiązaniem. Spróbuj deltę jeszcze raz.
26 kwi 18:42
dpelczar: racja

ma nie pomnożyłem 1 przez trzy...

wiec ostatecznie bedzie Δ= 5m
2 − 18m +9
5m
2−18 +9 < 0
(m −
35) (m −3) < 0
m=
35 m = 3
nie ma rozwiazan dla m∈(
35 ; 3)
teraz

26 kwi 18:51
tim: Już prawie. Dalej coś namieszałeś (złe znaki)
26 kwi 18:56
xpt: dpelczar − jeżeli Δ<0 to nie ma miejsc zerowych należących do zbioru liczb rzeczywistych.
Radzę, jesli podobne zadanie pojawi się na maturze, to zaznaczyć, bo odpowiedź jest
nieprecyzyjna.
26 kwi 19:02
dpelczar: o matko

ale dalem ciała...

ma być +18
m∈(−3 ;−
35)
26 kwi 19:10
tim: Teraz ok

26 kwi 19:10
tim: Chcesz jeszcze jedno? (z wart. bezwzględną i parametrem?) albo z jakiejś innej kategorii?
26 kwi 19:11
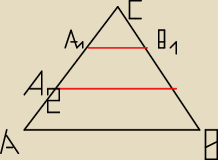
nana: Podstawa AB trójkata ma długość 24 cm. Na boku AC zaznaczono punkty A1, A2, a na boku Bc
punkty B1, B2 w taki sposób,że A1IIB1 i A2B2IIAB. Wiedząc, że IA1B1I=8cm, IA2B2I=20cm,
onlicz stosunek pól:
a) trójkątów A1B1C, A2B2C, ABC
b) figur A1B1C, A2B2B1A1 i ABB2A2
Proszę pomóż

))))
jak najszypciej, chodzi mi głównie o dobre rozpisanie....

)
Z góry dzięki

26 kwi 19:11
dpelczar: jesli Δ< 0 to są zespolone no ale na maturze wiadomo... ale zaznaczyc co ze jesli
mniejsza od zera to nie ma rozwiazan tak


26 kwi 19:11
dpelczar: Tim to dawaj wart bezwzg

26 kwi 19:12
tim: | | 2 | |
Dane jest równanie | |
| + 3| = p z niewiadomą x. Wyznacz liczbę rozwiązań tego |
| | x | |
równania w zależności od parametru p

Za 3−4 punkty. Jak wolisz

26 kwi 19:14
xpt: Jeżeli delta jest mniejsza od zera to nie ma rozwiązań w zbiorze liczb rzeczywistych.
Tak mi moja nauczycielka z liceum poradziła, a nie mógłbym powiedzieć, żeby kiedyś mi źle
doradziła

26 kwi 19:16
dpelczar:
26 kwi 19:17
dpelczar: Te trójkąty są podobne wiec stosunek podstaw bedzie odzwierciedlał ich pola wiec:
| |A1B1| | | P11C | |
| = |
| |
| |A2B2| | | P22C | |
26 kwi 19:20
dpelczar: XPT − rozumiem

wiec tak zrobie

26 kwi 19:20
dpelczar:
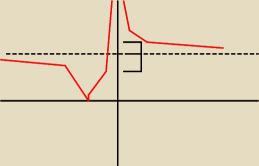
Tim masz to z arkuszy chyba


jedno rozwiazanie dla p = 0 i p=3
2 rozwiazania dla p ∈(0,3) u (3,+
∞)
26 kwi 19:28
dpelczar: nana wystarczy

poradzisz juz sobie

26 kwi 19:28
tim: A brak rozwiązań?

26 kwi 19:29
26 kwi 19:32
dpelczar: oczywiscie dla p (−
∞,0)



wiedziałem ze cos mi znajdzieszw rozwiazaniu


ale
w ten sposub sie naucze

26 kwi 19:33
tim: Jeszcze jakieś łatwe ci damy.
Dane są liczby:
Oblicz wartość bezwzględną liczby x = b − a − π
26 kwi 19:34
nana: prosze rozpisz dalej...

26 kwi 19:36
tim: Funkcja f(x) przyporządkowuje liczbom naturalnym (0,12) liczbę ich naturalnych
dzielników, bez 1 i samej siebie. Wykonaj wykres, tabelkę oraz podaj Df, Zwf, miejsca
zerowe, oraz oblicz wartość f(5) + f(3) − √f(4). Te dwa zadania NIE są z arkuszy.
26 kwi 19:37
tim: Co do 1. Wynik nie musi być obliczony, ale ma być w najprostszej postaci

26 kwi 19:39
dpelczar: NANA :
A
1B
1 = 8
A
2B
2 = 20
Reszta analogicznie...
Niech ktos policzy ci podpkt. b bo ja juz nie moge musze leciec... a jesli ci sie spieszy
to popros kogos

26 kwi 20:43
dpelczar: Ok zabiore sie za nie ale dopiero w nocy

bo musze isc... ale dizekuje

bo beda
ciekawe zadania

26 kwi 20:44
nana: ok dzięki wielki...

26 kwi 21:21
dpelczar: Tim nie rozumiem tresci zadania

staram sie czytam po kilka razy i nie wiem... i co
oznacza (0,12) −−> oznacza przedział

0, 1, 2, 3, 4... 11, 12
27 kwi 14:58
tim: Tak, oznacza przedział od (0,12)
27 kwi 15:00
tim: ale zawuaż, że przedział OTWARTY, czyli (0,12) (bez 0 oraz 12)

27 kwi 15:00
Bogdan:
Przedział (0, 12) oznacza zbiór wszystkich (nie tylko całkowitych) liczb od 0 bez zera
do 12 bez 12. Jest to przedział dwustronnie otwarty.
Uwaga: (0, 12) ≠ {0, 1, 2, ... 12}.
27 kwi 15:04
dpelczar: teraz rozumiem

bede kombinował

27 kwi 15:10
tim: Ale UWAGA! W poleceniu interesuje nas tylko naturalne!

27 kwi 15:12
Kasia.z: Dane są funkcje f(x)=3x2−5x i g(x)=(19)−2x2−3x+2. Oblicz dla których argumentów x wartość
funkcji f są większe od wartości funkcji g.
27 kwi 15:15
Kasia.z: w trójkącie ABC dane są: AB=8 BC=3 kąt ACB=60o. Oblicz objętość i pole powierzchni
całkowitej bryły powstałej po obrocie trójkąta dookoła boku BC
27 kwi 15:18
tim: Kasiu.. nie tu, tylko nowe zadanie utwórz.
27 kwi 15:19
dpelczar: to chyba nie zadania maturalne...

Narazie jem...

27 kwi 15:38
Michał Szczotka:): siostra mi przyniosła nowe dzisiaj to ci zaraz coś wkleje
27 kwi 15:43
Kasia.z: ależ to są zadania maturalne

proste są to wiem ale nie wiem jak zabrać się do
tego....naprowadźcie mnie trochę proszę resztę sama wykombinuje...
27 kwi 15:46
Kasia.z: wystąpił malutki błąd miało być:: Dane są funkcje f(x)=3x2−5x i
g(x)=19−2x2−3x+2. Oblicz dla których argumentów x wartości funkcji f są większe
od wartości funkcji g.
27 kwi 15:59
Kasia.z: Dane są funkcje f(x)=3x2−5x i g(x)=(19)−2x2−3x+2. Oblicz dla których
argumentów x wartości funkcji f są większe od wartości funkcji g
27 kwi 16:01
miśka: pomoze ktos mi z zadaniem ?
27 kwi 16:02
Michał Szczotka:): ja
27 kwi 16:28
Michał Szczotka:):
3
x2−5x>3
−2*(−2x2−3x+2)
nie ma nierówności wykładniczych na maturze

wiesz co dalej

?
27 kwi 16:31
27 kwi 16:36
tim: dpelczar dawaj

27 kwi 16:37
dpelczar: zrobie to

jak masz jeszcze jakis to dawaj

bede ok 21 i zamieszcze rozwiazania

27 kwi 16:37
tim: Ok.

27 kwi 16:39
Michał Szczotka:): ja szukam jakiegoś zadania ale znowu dostałem z pochodną albo jakimiś szeregami albo
indukcja a ty raczej delpczar tego nie umiesz co

? mogę ci jakieś przepisać ale coś co
na pewno umiesz to to
1.Usuń niewymierność z mianownika
2. Dla jakich wartości parametru k∈R równanie cos2x+2k=sinx ma przynajmniej jedno
rozwiązanie w przedziale (0;π)
Prosze 2 zadanka jak zrobisz to podam ci następne

27 kwi 16:43
Wito: Macie fajne zadanko z wielomianow:
Liczba 2 jest dwukrotnym pierwiastkiem W(x)=x4+ax3+bx2+20x−4. Wyznacz a i b. Dla
wyznaczonych a i b rozloz ten wielomian na czynniki
27 kwi 17:12
Kris_garg: 1.Usuń niewymierność z mianownika;
odpowiedz to :
1
− −−−−
2
√2

27 kwi 18:02
Kris_garg: dlej usuwając wychodzi
√2
−−−−−
4
27 kwi 18:05
miśka: pomoze ktos z zadaniem?
27 kwi 18:05
Michał Szczotka:): najpierw zastawów się o co chodzi w usuwaniu niewymierności z mianownika
27 kwi 18:06
miśka: pomoze ktos z moim zadaniem do konczyc?
27 kwi 18:07
miśka: bardzo prosze o szybka pomoc musze dokonczyc zad
27 kwi 18:08
miśka: jest ktos kto moze pomoc?
27 kwi 18:09
dpelczar: Umiem pochodne

z szeregami gorzej... indukcja − zalezy...

27 kwi 21:45
Mickej:
1. Dla jakich wartosci parametru a prosta o równaniu y=2x−a jest styczna do okręgu o
równaniu
x
2+y
2−4x−3y=0
2. Wyznacz ekstrema i przedział monotoniczności funkcji o równaniu
gdybyś nie wiedział jak to zrobić to pytaj
27 kwi 21:52
Mickej: Rozwiąż równanie
X3−2,5x2+5x−2=0
27 kwi 22:23
Mickej:
| | 1 | |
W jakim punkcie wykresu funkcji f(x)= |
| należy poprowadzić styczną do tego wykresu |
| | x3 | |
aby pole trójkąta ograniczonego tą styczną i osiami układu współrzędnych było równe
27 kwi 22:45
dpelczar: Z usunięciem niewy,mierności mam problem...

a zadanie drugie to wiec tak:
cos jest "ścieśniony" dwa razy a 2k podnosi wykres cos o jakąś wartość
sądze ze k ∈(0,1)
27 kwi 22:47
dpelczar: MICKEJ − policzyłem pochodną ale Δ<0 co teraz...


27 kwi 22:50
dpelczar: chodzi mi o zadanie x3 − 2.5x2+5x = 0
27 kwi 22:50
dpelczar: no tam na koncu jeszcze −2 jest

27 kwi 22:51
Mickej: nie gdzieś zrobiłeś błąd sprawdź jeszcze raz a ta niewymierność to jest po prostu cudo

27 kwi 22:51
Mickej: wystarczy skorzystać z twierdzenia o pierwiastkach wymiernych a nie pochodną machać

27 kwi 22:54
dpelczar: podpowiedz mi − kurde nie wiem czy mam gorszy dzisiaj dzien czy jestem taki słaby z matmy

27 kwi 23:10
Mickej: ale w którym zadaniu tym równaniu 3 stopnia

| | 1 | |
x= |
| jest pierwiastkiem |
| | 2 | |
27 kwi 23:12
dpelczar: dam sobie dzisiaj spokuj... jestem przemeczony... jutro zobacze na te zadania bo dzisiaj
idzie mi coraz gorzej...

27 kwi 23:26
Mickej: jeszcze mamy czas do matury jeszcze 2 tygodnie
27 kwi 23:27
dpelczar: ale normalnie nie moge sobie z tymi zadaniami poradzic... sadze ze bedzie zle u mnie z
matura...
ale mimo to dziekuje i prosze o pomoc w przygotowaniu sie do niej.. widze ze jestes dobry
i oblukany w matmie... ja osobiscie matematyke lubie i to bardzo... ale niepotrzebnie
sobie zmarnowalem caly rok i dopiero 2−3 mies przed matura zaczalem sie uczyc a tak na
prawde cos robiec z grobej rury to od 1mies i na tym forum zadania robic...
dzieki za zaangarzowanie

27 kwi 23:31
grazia: oblicz wartosci pozostalych funkcji trygonometrycznych wiedzac ze tgα=9/4 i ctgα=−4/9 czy
ktos mi to obliczy?dzieki
28 kwi 08:36
Mickej:
Wykaż, bez użycia kalkulatora i tablic, że
3√5√2+7−3√5√2−7 jest liczbą całkowitą
28 kwi 16:25
dpelczar: Mickej
Liczba całkowita to 14


28 kwi 16:50
Krzysiek: "5m2+18m +9 < 0
(m − 3/5) (m −3) < 0
m= 35 m = 3"
Sorry, ale co to jest? Od kiedy (m+3/5)(m+3)=5m2+18m+9
28 kwi 16:55
Mickej: 14 to liczba całkowita ale tutaj wynikiem jest 2 a nie 14

tylko licze na jakieś sensowne
rozwiązanie z twojej strony
28 kwi 17:05
Mickej: Krzysiek widział kiedyś postać iloczyn ową nie widział wiadome postać to
a(x−x
1)(x−x
2) teraz równe

?
28 kwi 17:08
dpelczar: Miałem pisać krzyśkowi własnie co do postaci iloczynowej.... wiem ze mialem pomyłki w znakach
ale wynik ostateczny(poprawiony) byl dobry

własnie mecze s sie z tymi pierwiastkami...

28 kwi 17:11
Krzysiek: aha, czyli tam po prostu w zapisie twoim nie ma tego a przed nawiasami, zapomniałem o czymś
takim. Nie łatwiej z tego 5m2+18m+9 wyliczyć deltę.
28 kwi 17:36
Mickej: nawet nie wiem o jakiej delcie mówcie

28 kwi 17:41
dpelczar: kurde zamieniałem to na potęgi niewymierne, cudowałem, i mi nie wyszło...
powiedz mi jak to zrobiłes...

28 kwi 17:52
Mickej:
robię sobie równanie że całe to wyrażenie = np k czy jakaś inna literka i na tym działam
podnosze do 3 i dalej to już ładniej wychodzi
28 kwi 17:55
dpelczar: to tak robiłem − podnosiłem do 3 potegi....ale nie dawałem niewiadomej k....
a po podniesieniu do potegi i tak sie pojawialo pierw. 3−topnia z ...... do kwadratu...

28 kwi 18:05
Mickej: doglądam housa i napisze ci rozwiązanie
28 kwi 18:25
dpelczar: MICKEJ:
| | 1 | |
W jakim punkcie wykresu funkcji f(x)= |
| |
| | x3 | |
należy poprowadzić styczną do tego wykresu
| | 8 | |
aby pole trójkąta ograniczonego tą styczną i osiami układu współrzędnych było równe |
| |
| | 27 | |
| | y | | 27y2 | | 16 | |
tgα = |
| = |
| = |
| |
| | | | 16 | | 27x2 | |
| | 1 | | 16 | |
i tu mam problem co dalej bo wyszło mi ze b = |
| − |
| |
| | x3 | | 27x | |
i teraz jak podstawie za wszystko do funkcji liniowej to mi sie normalnie skraca...
przynajmniej wiem ze nie ma błedu rachunkowego... ale co zrobic ... dalej...

28 kwi 18:35
Mickej:
3√5√2+7−
3√5√2−7=k \ ()
3
k
3=(
3√5√2+7)
3−3(
3√5√2+7)
2 3√5√2−7+3(
3√5√2+7)−(
3√5√2−7)
3
k
3=14−3
3√5√2+73√5√2−7(
3√5√2+7−
3√5√2−7)
i teraz
3√5√2+73√5√2−7=1 to chyba oczywiste dalej
3√5√2+7−
3√5√2−7=k to z początkowego podstawienia i otrzymujemy
k
3=14−3k a to ma tylko jedno rozwiązanie
k=2

28 kwi 18:50
dpelczar: jesli mozesz to pokarz mi ze 3√5√2+7 * 3√5√2−7 = 1 nie moge tego udowodnić... nie
wychodzi mi... do twojej pierwszej postaci doprowadziłem(brakuje ci tam jednego pierwiastka i
kwadratu...)
28 kwi 19:01
Mickej: no to nie widać czasem przy takich rzeczach a to to tak
3√a*3√b=3√ab
3√5√2+73√5√2−7=3√(5√2+7)(5√2−7) z różnicy kwadratów
3√50−49=3√1=1 a to drugie to nie teraz bo mnie tu słońce tak jara że zaraz kotka dostane
28 kwi 19:04
dpelczar: kurde ze nie wpadłem na to...

28 kwi 19:08
tim: 100!

28 kwi 19:08
dpelczar: ale fajne zadanie

teraz bede wiedział jak je rozgryść

28 kwi 19:08
dpelczar: 100 silnia

pytasz sie lie to jest


czy 100 postow

28 kwi 19:09
tim: To ostatnie

28 kwi 19:12
28 kwi 19:14
dpelczar: a mozesz mi pomoc z tym wykresem

bo stanąłem w miejscu...

28 kwi 19:18
dpelczar: | | 1 | |
Chodzi mi o zadanie ze styczną... i f(x) = |
| |
| | x3 | |
28 kwi 19:31
Mickej:
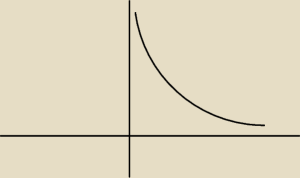
wykres jest nieparzysty więc dla x<0 wykres wygląda jak lustrzane odbicie
28 kwi 19:56
ciemny :(: MICKEJ dasz rade to zrobić

Albo tim... albo ktokolwiek

| | 1 | |
W jakim punkcie wykresu funkcji f(x)= |
| |
| | x3 | |
należy poprowadzić styczną do tego wykresu
| | 8 | |
aby pole trójkąta ograniczonego tą styczną i osiami układu współrzędnych było równe |
| |
| | 27 | |
28 kwi 20:12
dpelczar: widze ze ktos tez potrzebuje odpowiedzi na to zadanie ...


28 kwi 20:15
Mickej: wyznacz równanie kierunkowe prostej
f(x)={1}{x
3} a po co ci to zadanie

?
28 kwi 20:19
Mickej: | | 1 | |
f(x)= |
| nawet już mi ułamki nie wychodza |
| | x3 | |
28 kwi 20:20
Mickej: widzę że zero chęci
28 kwi 20:42
dpelczar: Nie wiem jak to zrobić a chęci mam sporo jak widaćze robie cokolwiek

tylko nie było mnie dluga chwile na kompie...
28 kwi 23:15
@Basia: Zadanie ze styczną.
Takich stycznych jest nieskończenie wiele.
prosta y = ax+b przecina oś OY w p−cie (0,b), oś OX w p−cie (−
ba;0)
16a = −27b
2
y = −
2716b
2x + b
dla b=1
y = −
2716x + 1
f'(x) = −
3x4
−
3x4 = −
2716
27x
4 = 16*3
x
4 =
169
x = ±
2√3 = ±
2√33
dla b=2
y = −
274x + 2
−
3x4 = −
274
27x
4 = 3*4
x
4 =
49
x = ±
4√49
itd.
ogólnie:
−
3x4 = −
27b216
1x4 =
9b216
| | 16 | | 24 | | 24 | |
x4 = |
| = |
| = |
| |
| | 9b2 | | 32b2 | | (3b)2 | |
gdzie b∊R\{0}
29 kwi 01:06
dpelczar: Teraz wiem jak sie za to zabrac...

Dziekuje BASIU

A czy mój poczatek rozwiazania był na dobrym tropie


A myślałem ze bedzie jedno rozwiazanie...
29 kwi 10:25
Tomek: Zadanie Maturalne.
Uzasadnij, że jeśli liczby x1, x2 są pierwiastkami równania ax2+bx+c=0, gdzie
ac≠0, to liczby 1/x1, 1/x2 są pierwiastkami równania cx2+bx+a=0
29 kwi 10:43
Kris_garg: z Vieta:
x1*x2= −b/a
1/x1 * 1/x2 = −b/a/c/a = −b/c
czyli ac≠0
Mam pytanie wie ktoś jak wyglada sprawa z tablicami matematycznymi(zestaw wzoró) na maturze
roz. ? do arkuszu egzaminujacy dostaje cale 19 stron jakie sa umieszczone na tej stronie
(Zestaw wzorów matematycznych z CKE)? czy tylko wybrane wzory zgodne z tresca zadan w tescie
maturalnym ?
29 kwi 11:16
Mickej: wszystkie wzory z CKE
29 kwi 11:18
♊: Krisgarg − mozesz zobaczyć jakie wzory są na tych tablicach − po lewej masz menu wybierz
"MATURA Z MATEMATYKI" i na dole masz link do zestawu wzorów.
29 kwi 11:49
Kris_garg: to dobra wiadomość dla mnie bo niekiedy zdarza mi się zapomnieć wzoru a tu go będę miał pod
ręką

aha i mam jeszcze jedno pytanie według tego artykułu NIE może sie pojaic żadne zagadnienie tu
wymienione w zdaniach maturalnych w tym roku ? Posiadam kilka ksiazek przygotowujacych
egzaminujacego do matury i tam polowa jak nie wiekszosc zadan jest z tymi zagadnieniami ? wiec
jak to bedzie tak naprawde bo juz tylko 14 dni a ja dalej nie jestem w 100 % pewny o co tu
chodzi ?
Od 1 września 2007 r. obowiązuje nowa podstawa programowa z matematyki. Różni się ona zakresem
treści od podstawy programowej obowiązującej wcześniej, według której uczona była młodzież,
która przystąpi do egzaminów w roku szkolnym 2008/2009. Mając to na uwadze, dyrektor CKE
ogłosił listę treści, które nie będą sprawdzane na maturze w 2009.
Na egzaminie maturalnym z matematyki na poziomie rozszerzonym nie będą sprawdzane poniższe
treści:
* Twierdzenie o rozkładzie liczby naturalnej na czynniki pierwsze.
* Wzór (a – 1)(1 + a +...+ an−1) = an −1
* Indukcja matematyczna.
* Różnowartościowość funkcji.
* Funkcje parzyste, nieparzyste, okresowe.
* Dwumian Newtona.
* Równania i nierówności wykładnicze i logarytmiczne.
* Nierówności trygonometryczne.
* Wzory redukcyjne.
* Przykłady ciągów zdefiniowanych rekurencyjnie.
* Pojęcie granicy ciągu.
* Obliczanie granic ciągów.
* Suma szeregu geometrycznego.
* Pojęcie funkcji ciągłej.
* Pojęcie pochodnej.
* Interpretacja geometryczna i fizyczna pochodnej.
* Obliczanie pochodnych wielomianów i funkcji wymiernych.
* Związek pochodnej z istnieniem ekstremów i z monotonicznością funkcji.
* Zastosowanie pochodnej do rozwiązywania problemów praktycznych.
* Przykłady przekształceń geometrycznych: obrót.
* Twierdzenie o związkach miarowych między odcinkami stycznych i siecznych.
* Wielościany foremne.
* Rzut prostokątny na płaszczyznę.
* Prawdopodobieństwo warunkowe.
* Wzór na prawdopodobieństwo całkowite.
* Niezależność zdarzeń.
* Schemat Bernoullego.
* Twierdzenie o trzech prostych prostopadłych.
29 kwi 12:27
♊: Książki z zadaniami nie są aktualizowane tak często, jak wymagania egzaminacyjne. Równie dobrze
może się zdarzyć tak, ze w przeddzien egzaminu cos się zmieni w wymaganiach (tak było na
przykład z maturą z języka angielskiego bodajże 2 lata temu).
Ja się i tak uczyłem całej podstawy programowej z liceum na maturę (bo nie chciało mi się przy
powtarzaniu sprawdzać co wywalili a czego nie :P ).
Jednak na chwilę obezną, jeśli nie ukazał się nowszy artykuł to ten jest ważny.
29 kwi 12:34
Mickej: to jest syf a nie bo za takie głupie zadanie z logarytmów albo wykładniczej czy pochodnej było
zawsze po 7 ,8 czy nawet 9 pkt a były proste a teraz dają jakieś kiczowate zadania za 4 pkt i
trzeba kombinować
29 kwi 12:44
Kris_garg: Mógłbyś podać przykład takiego zadania za 4 pkt ?
29 kwi 12:55
Kris_garg: Ja mam takie za (4 pkt) :
Rozwiaż równanie: sinx + √3cosx = 1 . Rozwiązania w przedziale <−π,2π>
29 kwi 12:58
29 kwi 13:00
Mickej: wszystkie zadanie obliczeniowe czyli funkcje logarytmy i jakieś inne pierdoły z ostatnich lat
robię jedynie z jakimi mam problemy to jakieś treściowe pipidułki
29 kwi 13:01
tim: A mam pytanie odnośnie nowej matury

od 2010 (tej obowiązkowej). Poziom podstawowy (jak
czytałem) będzie miał 20−30 zamkniętych, kilka za 2p oraz kilka 4−6 punktów. Czy poziom
rozszerzony również będzie miał tak samo, czy się nie zmieni?
29 kwi 13:02
Kris_garg: Wiem czytalem: tylko mam maly problem mianowice wyszło mi
sin( π/3 + x) = 1/2
xo= π/3 +x = π/6 = −π/6
x = −π/6 + 2kπ ?
i jak dalej z rozwiazaniami

29 kwi 13:04
Mickej: Zamknięte na Poziomie R

chyba kpisz poziom R się nie zmienia no jeszcze może wam
materiał obetną bo zaraz to jeszcze nawet funkcje zabiorą z matury
29 kwi 13:10
tim: Mickej.. A już myślałem, że tak dobrze będzie

. Mickej od 2012 (ja się załapię) mają
połowę obciąć materiału

29 kwi 13:12
Mickej: może zostawią chociaż równania liniowe i twierdzenie Pitagorasa to zdasz

29 kwi 13:15
Bogdan:
sinx +
√3cosx = 1
| | π | | | |
Podstawienie: √3 = tg |
| = |
| |
| | 3 | | | |
| | | | π | |
sinx + |
| * cosx = 1 mnożymy obustronnie przez cos |
| |
| | | | 3 | |
| | π | | π | | π | |
sinx cos |
| + sin |
| cosx = cos |
| |
| | 3 | | 3 | | 3 | |
| | π | | π | | π | | π | |
x + |
| = |
| + k*2π lub x + |
| = π − |
| + k*2π, k € C |
| | 3 | | 6 | | 3 | | 6 | |
| | −π | | π | |
x = |
| + k*2π lub |
| + k*2π |
| | 6 | | 2 | |
29 kwi 13:15
tim: No... Na podstawie ma być kolejność wykonywania działań 2+2*2 i dwa warianty

29 kwi 13:15
tim: 
Nie no żart

29 kwi 13:16
Kris_garg: w odp jest x { − π/6, π/2 i 1 5/6π ? } przedział przypominam <−π,2π>
29 kwi 13:27
Krzysiek: nie rozumiem tego przejścia:
| | π | | π | | π | |
sinxcos |
| +sin |
| cosx=cos |
|
|
| | 3 | | 3 | | 3 | |
na
| | π | | π | |
cos |
| =sin |
| na to wpadłem, ale co się dzieje z tymi cosinusami z lewej strony? |
| | 3 | | 6 | |
29 kwi 13:37
Mickej: z wzoru
sin(α+β)=sinαcosβ+sinβcosα

29 kwi 13:39
Bogdan:
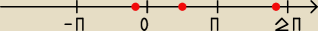
Komu przypominasz? Dokończ zadanie już sam. Wpasuj po prostu podane rozwiązania do podanego
przedziału przyjmując odpowiednią wartość k.
29 kwi 13:45
Krzysiek: heh, racja
29 kwi 13:52
dpelczar: Fajne zadanie − sam tez chwile myslalem skad było przejscie

29 kwi 14:08
Mickej: tak to jest jak się nie robiło zadanek przed maturą

29 kwi 14:11
dpelczar: Nie no... zadan troche robiłem...

ale czasem pomysłu brakuje albo czegos nie zauwaze...
29 kwi 14:17
dpelczar: f(x) 2sinx2x − sinx −1 Wyznacz zbior wartosci funkcji...
2sinx2 − sinx −(sin2x + cos2x )=0
2sin2x − sinx − sin2x − cos2x = 0
sin2x − sinx − cos2x = 0
nie wiem co teraz
sinx (sinx −1) − cos2x = 0 czy jak bo nie wiem
29 kwi 18:42
Mickej: a tam jest sin
2x czy sinx
2

29 kwi 18:44
Mickej: bo raz tak raz tak piszesz

29 kwi 18:44
dpelczar: sin
2x wszedzie

29 kwi 18:46
dpelczar:
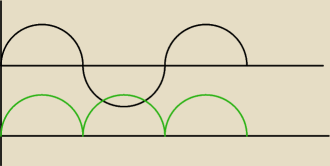
wiec powstanie po odjęciu
29 kwi 18:48
Mickej: no to ja robie na 2 sposoby
1. rysuje wykres i odczytuje z niego co i jak
2. robisz tak
sinx=t t∊<−1;1>
2t
2−t−1=0
i teraz pierwsze co robisz to sprawdzasz czy wierzchołek należy do przedziału <−1;1> jesli tak
to sprawdzasz jaką wartość przyjmuje następnie sprawdzasz dla skrajnych wartosci przedziału i
juz masz zbiór wartosci

29 kwi 18:48
dpelczar:
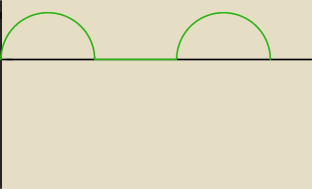
czy dobrze wysle


ale zostanie jeszcze wykres cos
2x... i nie wiem...
29 kwi 18:50
Mickej: jak zabierasz się za rysowanie to
2sin
x−sinx−1 to perfekcyjna postać nie przekształcaj

29 kwi 18:54
tak:

29 kwi 18:56
dpelczar:
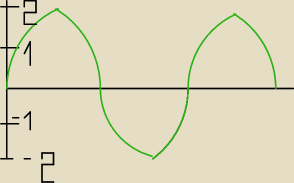
aaaa wiem ze juz zle mam... wykrs po odjeciu sin
2x − sinx to bedzie tak jak teraz mam wyzej ..

29 kwi 18:57
dpelczar: w sumie


29 kwi 18:58
Mickej: jak widze jak ty te wykresy rysujesz to normalnie
jak sin
2x−sinx może osiągać wartość −2

?
29 kwi 19:00
29 kwi 19:01
13LateK: wyznacz wszystkie wartości α (α≠kπ, keC), dla których trzy liczby ctgα, sinα, 16cosα, w
podanej kolejności tworza ciąg geometryczny
29 kwi 19:03
dpelczar: Mickej:
wyszło mi
2t
2 −t −1 =0
t
2 = 1
potem podstawiłem (−1) za t wyszło mi 2=0 czyli sprzeczne
za t podstawilem 1 i wyszło 0=0 czyli rownanie prawdziwe
z tego wnioskuje ze −1 nie nalezy do wykresy wiec t ∊ (−1, 1>
| | 1 | | π | | π | |
chyba ze mam zrobic tak − |
| = sinx −−−> x = − |
| i π− |
| + 2*k*π |
| | 2 | | 6 | | 6 | |
1 = sinx −−−−> x = 0 i x = π + k*π
ale nie wiem co dalej czy to wystarczy...
29 kwi 19:14
dpelczar: | | π | |
kurde.... sorryyy 1 = sinx −−−> x = |
| + 2*k*π przepraszam za pomyłke |
| | 2 | |
29 kwi 19:15
Mickej: nie tak patrz
wierzchołek
| | 1 | |
p= |
| czyli należy i dla tego argumentu będzie minimum bo ramiona skierowane do dołu |
| | 4 | |
wyznaczamy wierzchołek
q=−1
dla skrajnych wartosci to
f(−1)=2+1−1=2
f(1)=2−1−1=0 czyli zbióra wartosci to <−1;2>
29 kwi 19:18
dpelczar: | | 1 | |
aha ale dla P( |
| ; −1) to chyba max bedzie  |
| | 4 | |
29 kwi 19:22
dpelczar: kurcze to łatwiejszy algorytm takich zadan

29 kwi 19:23
Mickej:
−1 to raczej min a maks to 2
29 kwi 19:24
dpelczar: ale chodzi mi ze wierzchołek to bedzie wart max

a ty napisałes min i nie wiem

29 kwi 19:24
dpelczar: a teraz takie zadanko na 5pkt
| | x2+2x−6 | |
f(x) = |
| na przedziale < −4 , 1> |
| | x+5 | |
wyznacz najmniejsząi najwieksza wartosc

29 kwi 19:30
Mickej: nawet pochodnej nie trzeba robić

ale to nie teraz za 30 min to zrobie
29 kwi 19:32
dpelczar: ok bo wiem ze wart bedzie najmniejsza kiedy mianownik bedzie najwiekszy

a wartosc najwieksza kiedy mianownik bedzie najmniejszy

dobrze mysle

29 kwi 19:37
Mickej: nie koniecznie
29 kwi 19:38
dpelczar: aha bo licznik jest zmienny ...
29 kwi 19:40
Mickej: ekstrema należą do przedziału niestety więc trzeba pochodną machnij jeśli możesz
29 kwi 19:47
dpelczar: ok
29 kwi 19:49
dpelczar: pochodna wyszła
29 kwi 19:52
Kris_garg:
q=−1 ? czemu −1

Δ= −1
2 − 4 * 2 * −1 = 1+8 = 9
q= 9/ 4*−2 = −9/8

29 kwi 19:52
29 kwi 19:53
dpelczar: nie rozumiem Kris o co ci chodzi...

29 kwi 19:54
Kris_garg: poprzednie zadanie jak mu wyszyszło −1 = q ? przeciez Δ= 9 a = 2 wiec
q= 9/4*2 = 9/8 a nie −1

29 kwi 19:58
dpelczar: | | 9 | |
tak  ma być |
| ale juz takich małych błędów mu nie wytykałem − bo wiedziałem juz jakie |
| | 8 | |
jest rozwiazanie

29 kwi 20:00
dpelczar: MIckej ja musze isc bede dzisiaj ok 24

jak siedzisz do pozna to porobie jakies zadania

i
jeszcze raz dziekuje za pomoc

29 kwi 20:01
dpelczar: pochodną policzyłem ale co dalej... dokoncz kiedy mozesz narqa

29 kwi 20:02
Kris_garg: Przyjemne zadanko za 4 pkt:
W trójkącie ABC boki AB i AC mają odpowiedni długość 4 i 6 , a kąt przy wierzchołku A to 60.
Oblicz długość cześć dwusieczne kata BAC zawartej w trójkącie ABC ?
29 kwi 20:20
Mickej: brzydka ta pochodna ma być taka
| | (x2+2x−6)'(x+5)−(x2+2x−6)(x+5)' | |
f'(x)= |
| |
| | (x+5)2 | |
| | (2x+2)(x+5)−(x2+2x−6)1 | |
f'(x)= |
| |
| | (x+5)2 | |
funkcja wymierna osiąga ekstrema gdy licznik =0 czyli
x
2+10x+16=0
Δ=100−64=36
√Δ=6
badamy znak pochodnej i dla −8 osiąga min a dla −2 maksimum tylko że −8 nie należy do
przedziału więc musimy sprawdzić dla skrajnych wartosci naszego przedziału
29 kwi 20:23
Mickej: wyznaczyć bok BC z tw cosinusów pozostałe jeden kąt przy podstawie i dwysieczna
29 kwi 20:25
Kris_garg:
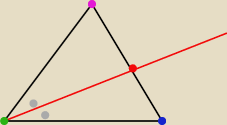
A nie lepiej Pabc= Pabd +Pacd
wzór P= 1/2absinα
Odp:
AD = 12
√3/5
29 kwi 20:34
Mickej: każdy robi jak lubi
29 kwi 20:36
Kris_garg: Zadanie za 3pkt:
Wyznacz równanie obrazu prostej l o równaniu 2x−3y−5=0 w jednokładności o środku S=(o,−3) i
skali k= −2 ?
29 kwi 20:39
Mickej: nie wiesz jak to zrobić czy dorzucasz zadania delpczarowi

?
29 kwi 20:40
Kris_garg: dziele sie zadaniami maturalnymi z innymi uczestnikami forum przy okazji można poznać kilka
rozwiązań jednego zadania

29 kwi 20:42
Mickej: to lepiej w poscie Koczera

tam wczoraj maturzyści machali
29 kwi 20:44
Kris_garg: Ide ogladać LM !
ARSENAL

Prawdopodobienśtwo że wygra arsenal moim zdaniem 90 %

narazie
29 kwi 20:48
Bogdan:
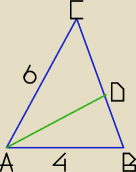
W sprawie dwusiecznej w trójkącie.
| | 12√3 | |
Wg Krisgarga |AD| = |
| ≈ 4,16. |
| | 5 | |
Jeśli |AB| = 4, to w omawianym trójkącie długość dwusiecznej AD jest mniejsza od 4.
29 kwi 21:18
POMOCY:
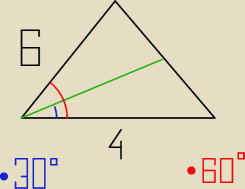
c
2 = 4
2 + 6
2 − 2*4*6* cos60
o
c
2 = 28
c = 2
√7
| | 4*0.9816 | |
s= |
| = 4.15 |
| | 0.9455 | |
Tak mi wyszło... ale powinno byc s<4 ale nie wiem...
30 kwi 00:05
gregory: ja mam zagadke

pewnie już ją ktoś tutaj widział ale napisze

a = b
a
2 = ab
a
2 − b
2 = ab − b
2
(a + b )( a − b ) = b( a − b )
a + b = b
2b = b
2 = 1
30 kwi 01:55
gregory: gdzie tutaj jest błąd

30 kwi 01:56
tim: Widz, s którym miejscu, ale nie wiem dlaczegO O.O
30 kwi 08:23
tim: Już wiem

30 kwi 08:27
Mickej: podzieliłeś przez 0 to nie zagadka
30 kwi 09:18
dpelczar: bez kalkulatora porównaj liczby:
| | sin19osin7o+sin71ocos367o | |
a= |
| |
| | 2sin282o | |
30 kwi 18:33
Mickej: sin71=cos19

cos367=cos7

to z pamięci przerobiłem ale chyba tak ma być
sin19sin7+cos19cos7=cos2=sin88
30 kwi 18:41
dpelczar: Moj login dpelczar − zmieniam nick na Damian

30 kwi 18:43
Mickej:
1. Rozwiąż układ równań
a)
b)
x+ay=b
ax−by=c
c)
|x
2−5|=1
x+y=5
2. Rozwiąż nierówność
a)
|x−2|<x+10
b)
|1−|x||≤3
| | f(2) | |
3. trójmian f(x)=ax2+bx+c ma pierwiastki −1 i 3 oblicz |
| |
| | f(1) | |
4. rozwiąż równanie, nierówność
a)
3x
6+4x
4+5x
2=0
b) x
5−4x
3−8x
2+32≥0
30 kwi 21:30
Mickej: Wyznacz wartość wyrażenia
log32*log43.......log109
30 kwi 21:31
Mickej: ostatni log ma być
log109
30 kwi 21:34
Wito: zamien wszystkie logarytmy, na logarytm z podstawa 10 i ladnie sie uprosci
30 kwi 21:40
Wito: i wyjdzie log102
30 kwi 21:42
Mickej: tu wrzuca się zadanka dla deplczara

bez podpowiedzi
30 kwi 21:42
Klara: 4 a)
x2( 3x4 +4x2 +5)=0
x = 0 −−− pierw. dwukrotny
w drugim delta < 0 −−− wiec nie ma pierw.rzeczywistych
b) x3( x2 −4) −8(x2 − 4)=0
( x 2 −4)( x3 − 8) =0
( x −2)(x +2)( x −2)( x2 +2x +4)=0
x= 2 x = −2 −− pierw. dwukrotny x2 +2x +4 −−− brak pierw. rzeczywistych
30 kwi 21:43
Wito: ok juz bede wiedzial
30 kwi 21:46
dpelczar: wiec robie

30 kwi 22:07
dpelczar: jesli sobie nie poradze to wtedy poprosze o pomoc

Układ równań
a)
(x+2)(y+1) − xy = 0
2y = −2 −x
(y−1)(x+3) = xy
3y−x−3 = 0
−6−3x = 2x+6
−5x = 12
30 kwi 22:12
dpelczar: | | 12 | |
zapomniałem minusa   ma byx x= − |
| |
| | 5 | |
30 kwi 22:25
Eto Klara: 
dla pewności podstaw i sprawdź

30 kwi 22:29
dpelczar: układ b)
x+ ay = b
ax −by=c
| 1 a |
det | a −b | = −b−a2
det1 = b a = −b2 −ac
c −b
det2 = 1 b = c − ab
a c
30 kwi 22:47
dpelczar: układ c)
|x
2 −5| =1
x+y =5
x
2 −5 = 1 x
2 +5 ≥0
−(x
2 −5) =1 x
2+5 <0
x =
√6 v x=−
√6
x
2 = 4
x= 2 v x= −2
x = 5 −y
|(5−y)
2 −5| = 1
(5−y)
2 −5 =1
−[(5−y)
2 −5] =1
y
2 −10 +19 =0
√Δ = 2
√6
y
1 = 5 −
√6
y
2 = 5+
√6
pary liczb
x =
√6 y=5−
√6 oraz
x=−
√6 y = 5+
√6
spełniają te rownania

DOBRZE

30 kwi 23:10
dpelczar: dla x =2 i x=−2 nie pisalem bo oczywiste ze wtedy równania wyjdą sprzeczne

wiec nie pisalem
w rozwiazaniu bo dyza zabawy


30 kwi 23:17
Michał Szczotka:
gdy x=2 lub x=−2 uzyskujemy podstawiająć do x+y=5
x=2 x=−2
y=3 y=7

30 kwi 23:17
Michał Szczotka:
|2
2−5|=1
|−1|=1
2+y=5 ==>y=3

30 kwi 23:19
Michał Szczotka: Zbadaj monotoniczność ciągu
30 kwi 23:22
Damian: ok zrobie je za chwile idem jesc

30 kwi 23:24
Klara:
zad/ dla jakiej wartości parametru "k"
równanie: I 11 − x2I =k ma trzy rozwiazania
1 maj 00:03
Bogdan:
Klaro, stosuj przy ułamkach dużą literę U
1 maj 00:06
Klara: Tak Bogdanie , wiem ale chodziło mi o moduł całego ułamka

1 maj 00:12
1 maj 00:13
Damian: | | |1| | | 1 | |
czyli chodziło ci o |
| = k ale ze to to samo co |
| = k |
| | |1−x2| | | |1−x2| | |
to rozumiem o co chodzi

zaczne te zadania rano robic bo jstem juz padniety...

1 maj 01:10
Michał Szczotka: dla k=1

są 3 rozwiązania

1 maj 11:13
Klara: 
1 maj 12:17
Michał Szczotka: wygrałem cukierka za rozwiązanie

1 maj 12:18
Klara: <mars>

1 maj 12:20
Klara: Witam

Zad: Dla jakich wartości parametru "m"
proste y = x +m i y = mx − 4 przecinają się w punkcie należącym
do symetralnej odcinka AB o końcach : A(1,1) B( − 3, 5)
1 maj 12:43
Kris_garg: Wykaż że jeśli a, b , c sa dlugościami boków trójkąta, to długość srodkowej Sa, opuszczonej na
bok o długości a wyraża się wzorem : Sa= 1/2 √2b2 + 2c2 − a2 ?
1 maj 13:06
Klara:
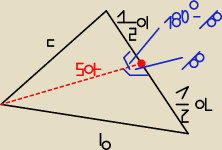
Zastosuj wzór cosinusów"
c
2 =(
12a)
2 +s
a2 − 2*
12a*s
a*cos(180
o− β) =
a24 + s
a2 +a*s
a*cosβ
podobnie:
b
2 = (
12a)
2 + s
a2 − 2*
12a*s
a*cosβ=
a24 +s
a2 − a*s
a *cosβ
dodając stronami obydwa równania otrzymasz:
c
2 + b
2 = 2s
a2 +
12a
2
dalej juz tylko przekształć i oblicz I s
aI
1 maj 13:39
Kris_garg: możesz mi to wytłumaczyc jaśniej jak − 2 * 1/2a = a ? czemu nie −a ? i gdzie i jak uprościło
się to 180 − β ?
1 maj 13:54
Klara: cos( 180o − β) = − cosβ −− ze wzorów redukcyjnych ( IIćw więc os ujemny)
wiesz już ?
1 maj 13:58
Kris_garg: ok ale dlalej nie umiem tego przeksztalcic do tej postaci z tresci zdania ? nie wychodzi mi to
samo

1 maj 14:15
Kris_garg: Sa= c + b − a czyli Sa= 1/2 √2b2 + 2c2 − a2 ? tak ?
1 maj 14:20
Damian: Rozwiazanie nierówności od Michała....
|x−2| − x−10 < 0
w przedziale (−
∞,2>
−(x −2) −x −10 <0
−x +2 −x −10 <0
−2x <8
x >4
w (2;+
∞)
x −2 −x −10 <0
−12 <0
z tego wynika ze w przedziale (2;+
∞) nierówność x−2 −4 −10 <0 ma nieskonczenie wiele rozwiazań
Dobrze myśle

Biorąc pod uwagę że w ogóle myślę


1 maj 14:21
Damian: Nierówność − kolejna od Michała


|1−|x|| ≤3 założenie |x|≥0 − zawsze wiec
|1−x|≤3 1−x ≥0
x≤1
|1−x| ≤ 3 ⋀ |1−x| ≥ −3
1−x ≤ 3 1−x ≥ −3
−x ≤ 2 −x ≥−4
x ≥ −2 x ≤ 4
x∊ <−2 ; 4>

Zgadza się

1 maj 14:29
Kris_garg: Zad. za (6 pkt.)
Narysuj wykres
1−|x|
f(x)= −−−−−−−−−
|x| −2
Korzystajac z wykresu funkcji f:
−odczytaj dla jakich argumentów funkkcja f przyjmuje wartści dodatnie
−wyznacz wszystkie wartości parametru k, dla ktorych równanie f(x) = k jest sprzeczne
1 maj 14:39
Michał Szczotka: wpadłem na 5 min i spadam dalej prezentacji się uczyć co do moich nierówności
|x−2|<x+10
Lewa strona jest zawsze dodatnia więc dla ujemnej strony prawej nierówność nie ma sensu więc
gdy x<−10 równanie nie ma sensu sprawdźmy
dla x≥−10
|x−2|<x+10 podnosimy obu Stronnie do kwadratu możemy ponieważ obie strony w rozpatrywanym
przedziale ≥0 i uzyskujemy
x2−4x+4<x2+20x+100
24x>−96
x>−4
a skoro rozpatrywaliśmy w przedziale x≥−10 i x wyszedł nam x>−4 to rozwiązaniem jest
x∊(−4;∞)
co do drugiej to ja to robię tak
korzystając z tożsamości
|x|≤a
−a≤x≤a uzyskujemy
−3≤1−|x|≤3
−4≤−|x|≤2 mnożymy przez(−1)
−2≤|x|≤4 |x| zawsze większe od −2 więc nie ma sensu rozpatrywać
|x|≤4
−4≤x≤4
odp x∊<−4;4>
1 maj 14:52
Kris_garg: Nie potrafie tego narysować
dla x<2,
∞)
1−x
f(x) =−−−−−−−
x−2
dla x(−
∞,−2>
1+x
f(x)= −−−−−−−
−x−2

1 maj 14:53
Damian: Od Michała:
3x
6 + 4x
4 + 5x
2 =0
x
2 (3x
4 + 4x
2 + 5) = 0 x
2 = t
t(3t
2 + 4t + 5) = 0
t= 0 v 3t
2 + 4t + 5 = 0
Δ = 16 − 60 = −44
I co teraz






Jeżeli pochodna to]
3t
2 + 4t +5 = 0
6t + 4 = 0
6t = −4
i co teraz

POmoże mi ktos z tymi końcówkami zadań


1 maj 14:53
Damian: Michał

czyli mam źle


bo jak sprawdziłem przedział <−2 ; 4> to sie zgadzało...


chodzi mi o pierwszą wart. bezwzględna

1 maj 14:57
Damian: Kros Garg...
|x|−2 ≠ 0 wiec x≠ −2 i x ≠2
zaraz napisze reszte ...

jak potrafie

1 maj 15:00
Michał Szczotka: brakuje ci w rozwiązaniu przedziału bo ty masz
<−2;4> a rozwiązaniem jest <−4;4> będę za godzinę jak by co
1 maj 15:07
Damian: Kolejne zadanko od MICHAŁA
| 1−x | | −(−1+x) | | (x−2)−1 | | −(x−2) | | 1 | | 1 | |
| = |
| = |
| = |
| − |
| = − |
| − 1 |
| x−2 | | x−2 | | x−2 | | x−2 | | x−2 | | x+2 | |
| 1+x | | (x+2)−1 | | x+2 | | 1 | | 1 | |
| = |
| = |
| − |
| = |
| + 1 |
| −x−2 | | −(x+2) | | −(x+2) | | −(x+2) | | x+2 | |
| 1 | | 1 | | 1 | |
| −−[SOX]−−> − |
| −−>[2,−1]−−> |
| +1 |
| x | | x | | x−2 | |
Dobrze


1 maj 15:20
Damian: Plissss powiedzcie ze dobrze...

bo sie staram jak moge ...

a jesli zle to powiedzcie
gdzie jest błąd...

1 maj 15:21
Damian: Przepraszam o zadanie było od Krisa

1 maj 15:22
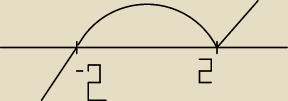
Damian: zadanie od MICHAŁA
x5 − 4x3 −8x2 + 32 ≥0
x3(x2 −4) −8 (x2 − 4) ≥0
(x3 −8)(x2 −4)≥0
x = 2 x=2 x=−2
1 maj 15:27
Damian:
1 maj 15:29
Damian: x≥0 ⇔ x∊<−2,2> ⋃ <2,+
∞) ⇒ x∊<−2,+
∞)
Mam rację


popatrzcie na moje rozwiazania czy robie dobrze prosze...

1 maj 15:31
Damian: Zadanie z logarytmami... zamieniłem podstawy − wszystko sie uprosciło i wyszło log10 2
1 maj 15:39
Bogdan:
Dobrze Damian, ale trzeba dopisać:
(x3 −8)(x2 −4) ≥ 0
(x − 2)(x2 + 2x + 2)(x − 2)(x + 2) ≥ 0
(x − 2)2(x + 2)(x2 + 2x + 2) ≥ 0
1 maj 15:42
Damian: Klaro zad 4 b) wyszlo nam podobnie ale wydaje mi sie ze masz błąd...

bo pierw. dwukrotnym
jest "2" a trzykrotnym jest "−2"

1 maj 15:42
Damian: hmmm Bogdanie... czyli −2 jest podwójnym miejsc. zerowym

hmmm czyli wykres mam zle...

własnie dochodze do tego co napisałes...

1 maj 15:46
Damian: aaaaaa

juz wiem

2 jest podwójnym a −2 pojedynczym − znaki mi sie pomyliły jak
patrzyłem na twoje rozwiazanie

CZYLI MAM DOBRZE

jupi

1 maj 15:47
1 maj 15:48
Damian: a Bogdanie mam pytanie
Jesli nie napisze takiej formy jak ty mi właśnie pokazałes, ale dobrze narysuje wykres i
zaznacze przedziały prawidłowo to uznają mi to na maturze jako dobre rozwiazanie czy
niepełne

1 maj 15:52
Damian: Zadanie z ciągiem
Zbadaj monotoniczność ciągu:
| | (n+1)! (n+2)(n+3)(n+1) | | n!(n+1)2(n+2)(n+3) | |
an+1 = |
| = |
| |
| | 5n+1 | | 5n *5 | |
| an | | n!(n+1)(n+2)n | | 5n * 5 | | 5n | |
| = |
| * |
| = |
| |
| an+1 | | 5n | | n! (n+1)2(n+2)(n+3) | | (n+3)(n+1) | |
Tylko teraz nie wiem co zrobić...

sprawdzic czy wynik jest ≥0 czy co....

1 maj 16:23
Michał Szczotka:
monotoniczność ciągu badamy w następujący sposób
a
n−a
n−1<0
gdy spełniona jest nierówność ciąg jest rosnący gdy jest sprzeczna ciąg jest malejący
a gdy wychodzi nam 0 po obu stronach nierówności ciąg jest stały

1 maj 16:28
1 maj 16:29
Bogdan:
Damianie, jeśli na rysunku zaznaczysz liczby −2 oraz 2, to musisz wcześniej je wyprowadzić
rachunkowo i trzeba te rachunki pokazać.
1 maj 16:29
Damian: Rozumiem

juz licze dalej

1 maj 16:40
Bogdan:
| | (n + 3)! (n + 1) | | (n + 2)! (n + 3) (n + 1) | |
an+1 = |
| = |
| |
| | 5n+1 | | 5 * 5n | |
| | (n + 2)! (n + 3) (n + 1) | | (n + 2)! n | |
Badamy znak różnicy: an+1 − an = |
| − |
| = |
| | 5 * 5n | | 5n | |
| | (n + 2)! | | (n + 3)(n + 2) | |
= |
| * ( |
| − 1) = ... |
| | 5n | | 5 | |
Jeśli a
n+1 − a
n > 0 to ciąg a
n jest rosnący,
jeśli a
n+1 − a
n < 0 to ciąg jest malejący.
1 maj 16:41
Damian: czyli moge zrobić tak...
an+1 − an >0
1 maj 16:42
Damian: aha rozumiem

1 maj 16:42
Damian: wyszło mi takie cosik....
| n! (n+1)2(n+2)(n+3) − n!(n+1)(n+2) n*5n | |
| >0 5n * 5 >0 |
| 5n *5 | |
n!(n+1)(n+2) [ (n+1)(n+3) − n*5
n ]>0
n!(n+1)
2(n+2)(n+3) − n! (n+1)(n+2) * n5
n > 0
n!(n+1)(n+2) [(n+1)(n+3) − n5
n] > 0
n! (n+1)(n+2) = 0
n! =0 n=−1 n = −2 (n+1)(n+3) − n5
n = 0
n=0 n
2+4n+3 − n5
n = 0
n
2 + 4n + 3 nie ma pierw w zbiorze liczb rzeczywistych
−n*5
n = 0 5
n > 0
−n = 0
n=0
Nie wiem czy jest dobrze... oceńcie co i jak...

1 maj 16:58
Damian: mam rysować wykres wielomianu


1 maj 17:00
Michał Szczotka: nie nie

przy ciągach się nie rysuje

nie możesz z nierówności przechodzić na równość
przyrównując coś do zera

są 2 sposoby rozwiązywania takich zadań książkowy ten który
zaproponował Bogdan albo taki bardziej nie książkowy jak ci podawałem tylko przy moim gdy coś
opuszczasz to zawsze uzasadniaj dlaczego tak robisz:0
1 maj 17:37
Damian: Ale.... nie potrafie....

nie łapie

1 maj 17:47
Damian: Po prostu sie gubie ...
1 maj 17:47
Michał Szczotka: ja spadam na grila

pamiętam że jakiś czas temu było parę zadanek tego typu na forum
poszukaj

ładnie rozwiązane były

jeśli nie znajdziesz to ja rozhukam to zadanko

1 maj 17:50
Bogdan:
| (n + 2)! | | (n + 3)(n + 2) | |
| * ( |
| − 1) = |
| 5n | | 5 | |
| (n + 2)! | | (n + 3)(n + 2) − 5(n + 3)(n + 2) | |
| * |
| = |
| 5n | | 5 | |
| (n + 2)! | | (n + 2)! | |
| * (−4*(n + 3)(n + 2))= −4 * |
| * (n + 3)(n + 2) < 0 |
| 5*5n | | 5*5n | |
| | (n + 2)! | |
ponieważ: −4 <0, |
| > 0, (n + 3)(n + 2) > 0, n ∊ N+ |
| | 5*5n | |
Ciąg a
n jest malejący.
1 maj 17:55
Damian: Panie Bogdanie a nie moge wpasc skąd sie wzięła druga linijka... zamiana −1 na ułamek ale jak

1 maj 18:21
Michał Szczotka: to jest błąd każdemu zdarzają się pomyłki

1 maj 22:11
Damian: Możę pan wytłumaczyc


Nie moge do tego dojsc

1 maj 22:11
Bogdan:
Proszę wykonać działanie: x − 5x =
1 maj 22:17
Damian: x − 5x = −4x
1 maj 22:20
Bogdan:
To niech x = (n + 3)(n + 2).
(n + 3)(n + 2) − 5(n + 3)(n + 2) = proszę dokończyć
1 maj 22:22
Damian: 
teraz juz wiem

DZIĘKUJE

wynik to −4(n+3)(n+2)
1 maj 22:29
Bogdan:
Tak i nie ma błędu, jak sugerował Michał.
1 maj 22:33
Klara: Witam

poprawimy:
a
n= U{(n+2)!*n}{5
n
| | (n+2)!*(n+3)(n+1) | |
an+1= |
|
|
| | 5*5n | |
zatem różnica a
n+1 − a
n =
| | (n+2)!*n | |
= U{(n+2)!*(n+3)(n+1)}{5*5n − |
| =
|
| | 5n | |
| | (n+2)! | | (n+3)(n+1) | |
= |
| *( |
| − n)=
|
| | 5n | | 5 | |
| | (n+2)! | | n2 +5n +3 − 5n | |
= |
| *( |
| =
|
| | 5n | | 5 | |
wyrażenie ( n+2)! >0
5
n >0
n
2 +3 >0
5>0
więc cała róznica >0 −−− zatem ciąg jest rosnący

1 maj 22:39
Damian: nie mowiłem nic obłędzie tylko nie wiedziałem co z czego...


1 maj 22:39
Bogdan:
Witam Klaro, co tak późno się pojawiasz. Uwijam się tu dzisiaj jak w ukropie, no i uciekło
mi
n. Dziękuję za poprawienie.

1 maj 23:33
Klara: Witam Bogdanie, dzisiaj Świeto Pracy

Majówkę zaliczyłam

...... teraz patrzę jak się uwijasz

Cześć pracy



1 maj 23:38
Kris_garg: Witam
Zadanie (6pkt.) :
Przekrój stożka wyznaczony przez wierzchołek i cięciwę podstawy jest trójkątem równobocznym o
polu 16√3. Płaszczyzna tego przekroju tworzy z płaszczyzną podstawy stożka kąt o mierze π/4,
Oblicz objętość stożka?
2 maj 10:36
Kris_garg: Zadanie (4pkt.):
Wykaż że jeśli suma częściowa ciągu (an) wyraża się wzorem Sn= n(2n−3) dla n∊N, to ciąg an jest
ciągiem arytmetycznym.
2 maj 10:39
Michał Szczotka: no fakt nie są trudne tylko w drugim zastanawiam się co oznacza suma częściowa

cienko u mnie
z taką teorią ale wykazać bym wykazał

2 maj 10:42
Kris_garg: Zadanie (4pkt.)
W okrąg o promieniu długości r wpisano kwadrat, w który następnie wpisano okrąg, a w ten okrąg
znowu wpisano kwadrat itd. Oblicz sumę pól wszystkich wpisanych kwadratów?
2 maj 10:56
Kris_garg: Zadanie (6 pkt.):
Graniastosłup prawidłowy trójkątny, w którym krawędź podstawy ma długość 12 cm, a wysokość 9
cm, przecięto płaszczyzną przechodzącą przez krawędź podstawy dolnej i środki wóch krawędzi
podstawy górnej. Oblicz pole otrzymanego przekroju i miarę kąta nachylenia przekroju do
płaszczyzny podstawy?
2 maj 11:08
Kris_garg: Zadanie (9 pkt.) :
Rozwiąż nierówność:
2−sinx + 4−sinx + 8−sinx + ... ≥ 0,(9)
2 maj 11:11
Michał Szczotka: to z kwadratem odpada na na maturze nie ma szeregu geometrycznego ostatnie tak samo

2 maj 11:41
Krzysiek: Jezscze co do zadania z ciągiem to:
| | (n+2)!*(n+3)(n+1) | |
an+1= |
|
|
| | 5n*5 | |
| | (n+2)! | |
więc skąd potem przy mnożeniu jest an= |
| gdzie się podziało jedno n?
|
| | 5n | |
| | (n+3)(n+1) | |
an+1= |
| −n tu to już w ogóle nie wiem co sięstało... |
| | 5 | |
2 maj 11:51
Michał Szczotka: jak się nie wie skąd się coś wzięło to się robi po swojemu miałem to zadanie na sprawdzianie
kiedyś i zrobiłem je na max pkt

ja np nie rozumiem w rozwiązaniu Bogdana dlaczego
| n+2)! | | (n+3)(n+2) | | n+2)! | | (n+3)(n+2)−5(n+3)(n+2) | |
| * ( |
| −1)= |
| *( |
| ) |
| 5n | | 5 | | 5n | | 5 | |
przecież jeśli próbował bym to rozbić to
| (n+3)(n+2)−5(n+3)(n+2) | | (n+3)(n+2) | |
| ≠ |
| −1 |
| 5 | | 5 | |
ale może tylko mi się wydaje
2 maj 12:10
Bogdan:
Michale, uciekło mi n.
Zobacz wyżej wpis Klary (ten z czerwoną literką n).
2 maj 14:39
@Basia:
Zadanie kris−garg
2
−sinx + 4
−sinx + 8
−sinx + ... ≥ 0,(9)
Lewa strona jest sumą nieskończoną ciągu geometrycznego, w którym
|q|<1
2
sinx>1
2
sinx>2
0
sinx>0
x∊⋃
k∊ℂ(0+2kπ; π+2kπ)=⋃
k∊ℂ(2kπ; 3kπ)
wtedy i tylko wtedy można zastosować wzór na sumę nieskończoną
dla wszystkich pozostałych x czyli x∊⋃
k∊ℂ<kπ; 2kπ>
nierówność jest spełniona ponieważ
| | 1 | |
q= |
| >1 czyli suma S=+∞ |
| | 2sinx | |
a +
∞ > 0,(9)
Prawa strona jest sumą nieskończoną ciągu
0,9 + 0,09 + 0,009+........
czyli geometrycznego, w którym
a
1 = 0,9
q = 0,1
dalej już sobie poradzicie
2 maj 15:15
Kris_garg:
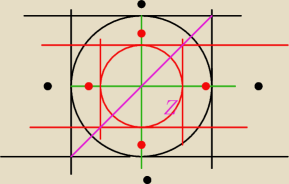
Zadanie z kwadratem :
d= a
√2
r= 1/2a
√2
1/2a
√2= r / 1/2
a
√2= r/2
a=r
√2
a1(czarna kropka) =r
√2 a q=
√2/2
czyli P= a
2 = 2r
2 , q
2= (
√2/2)
2 = 1/2
gdzie |q|< 1
a1
S= −−−−−− = 2r
2 * 2/1 = 4r
2
1− q
3 maj 11:19


 to jest maturalne.
to jest maturalne.
 mx2 − 3(m + 1)x + m = 0
Dla jakich m równanie nie ma rozwiązań w zbiorze rzeczywistych
mx2 − 3(m + 1)x + m = 0
Dla jakich m równanie nie ma rozwiązań w zbiorze rzeczywistych 


 licze delte i wychodzi 5m2 + 6m +1 < 0 (bo wtedy nie ma rozwiązań = miejsc zerowych)
5m2 + 6m +1 < 0
(m + 1)( m + 15) < 0
m= −1 m=−15
równanie nie ma rozwiazania dla m ∈ (−1 ; 15)
zgadza sie
licze delte i wychodzi 5m2 + 6m +1 < 0 (bo wtedy nie ma rozwiązań = miejsc zerowych)
5m2 + 6m +1 < 0
(m + 1)( m + 15) < 0
m= −1 m=−15
równanie nie ma rozwiazania dla m ∈ (−1 ; 15)
zgadza sie
 Metoda ok, ale gorzej z rozwiązaniem. Spróbuj deltę jeszcze raz.
Metoda ok, ale gorzej z rozwiązaniem. Spróbuj deltę jeszcze raz.
 ma nie pomnożyłem 1 przez trzy...
ma nie pomnożyłem 1 przez trzy...  wiec ostatecznie bedzie Δ= 5m2 − 18m +9
5m2−18 +9 < 0
(m − 35) (m −3) < 0
m= 35 m = 3
nie ma rozwiazan dla m∈(35 ; 3)
teraz
wiec ostatecznie bedzie Δ= 5m2 − 18m +9
5m2−18 +9 < 0
(m − 35) (m −3) < 0
m= 35 m = 3
nie ma rozwiazan dla m∈(35 ; 3)
teraz
 ale dalem ciała...
ale dalem ciała... ma być +18
m∈(−3 ;−35)
ma być +18
m∈(−3 ;−35)

 ))))
jak najszypciej, chodzi mi głównie o dobre rozpisanie....
))))
jak najszypciej, chodzi mi głównie o dobre rozpisanie.... )
Z góry dzięki
)
Z góry dzięki



 Za 3−4 punkty. Jak wolisz
Za 3−4 punkty. Jak wolisz 


 wiec tak zrobie
wiec tak zrobie 
 Tim masz to z arkuszy chyba
Tim masz to z arkuszy chyba 
 jedno rozwiazanie dla p = 0 i p=3
2 rozwiazania dla p ∈(0,3) u (3,+∞)
jedno rozwiazanie dla p = 0 i p=3
2 rozwiazania dla p ∈(0,3) u (3,+∞)
 poradzisz juz sobie
poradzisz juz sobie






 wiedziałem ze cos mi znajdzieszw rozwiazaniu
wiedziałem ze cos mi znajdzieszw rozwiazaniu 
 ale
w ten sposub sie naucze
ale
w ten sposub sie naucze 



 bo musze isc... ale dizekuje
bo musze isc... ale dizekuje  bo beda
ciekawe zadania
bo beda
ciekawe zadania 

 staram sie czytam po kilka razy i nie wiem... i co
oznacza (0,12) −−> oznacza przedział
staram sie czytam po kilka razy i nie wiem... i co
oznacza (0,12) −−> oznacza przedział 0, 1, 2, 3, 4... 11, 12
0, 1, 2, 3, 4... 11, 12

 bede kombinował
bede kombinował 

 Narazie jem...
Narazie jem... 
 proste są to wiem ale nie wiem jak zabrać się do
tego....naprowadźcie mnie trochę proszę resztę sama wykombinuje...
proste są to wiem ale nie wiem jak zabrać się do
tego....naprowadźcie mnie trochę proszę resztę sama wykombinuje...
 wiesz co dalej
wiesz co dalej ?
?




 jak masz jeszcze jakis to dawaj
jak masz jeszcze jakis to dawaj  bede ok 21 i zamieszcze rozwiazania
bede ok 21 i zamieszcze rozwiazania 

 ? mogę ci jakieś przepisać ale coś co
na pewno umiesz to to
1.Usuń niewymierność z mianownika
? mogę ci jakieś przepisać ale coś co
na pewno umiesz to to
1.Usuń niewymierność z mianownika


 z szeregami gorzej... indukcja − zalezy...
z szeregami gorzej... indukcja − zalezy... 
 a zadanie drugie to wiec tak:
cos jest "ścieśniony" dwa razy a 2k podnosi wykres cos o jakąś wartość
sądze ze k ∈(0,1)
a zadanie drugie to wiec tak:
cos jest "ścieśniony" dwa razy a 2k podnosi wykres cos o jakąś wartość
sądze ze k ∈(0,1)











 tylko licze na jakieś sensowne
rozwiązanie z twojej strony
tylko licze na jakieś sensowne
rozwiązanie z twojej strony
 ?
?
 własnie mecze s sie z tymi pierwiastkami...
własnie mecze s sie z tymi pierwiastkami... 







 teraz bede wiedział jak je rozgryść
teraz bede wiedział jak je rozgryść 
 pytasz sie lie to jest
pytasz sie lie to jest
 czy 100 postow
czy 100 postow 




 bo stanąłem w miejscu...
bo stanąłem w miejscu...
 wykres jest nieparzysty więc dla x<0 wykres wygląda jak lustrzane odbicie
wykres jest nieparzysty więc dla x<0 wykres wygląda jak lustrzane odbicie
 Albo tim... albo ktokolwiek
Albo tim... albo ktokolwiek 


 ?
?
 tylko nie było mnie dluga chwile na kompie...
tylko nie było mnie dluga chwile na kompie...
 Dziekuje BASIU
Dziekuje BASIU  A czy mój poczatek rozwiazania był na dobrym tropie
A czy mój poczatek rozwiazania był na dobrym tropie
 A myślałem ze bedzie jedno rozwiazanie...
A myślałem ze bedzie jedno rozwiazanie...
 aha i mam jeszcze jedno pytanie według tego artykułu NIE może sie pojaic żadne zagadnienie tu
wymienione w zdaniach maturalnych w tym roku ? Posiadam kilka ksiazek przygotowujacych
egzaminujacego do matury i tam polowa jak nie wiekszosc zadan jest z tymi zagadnieniami ? wiec
jak to bedzie tak naprawde bo juz tylko 14 dni a ja dalej nie jestem w 100 % pewny o co tu
chodzi ?
Od 1 września 2007 r. obowiązuje nowa podstawa programowa z matematyki. Różni się ona zakresem
treści od podstawy programowej obowiązującej wcześniej, według której uczona była młodzież,
która przystąpi do egzaminów w roku szkolnym 2008/2009. Mając to na uwadze, dyrektor CKE
ogłosił listę treści, które nie będą sprawdzane na maturze w 2009.
Na egzaminie maturalnym z matematyki na poziomie rozszerzonym nie będą sprawdzane poniższe
treści:
* Twierdzenie o rozkładzie liczby naturalnej na czynniki pierwsze.
* Wzór (a – 1)(1 + a +...+ an−1) = an −1
* Indukcja matematyczna.
* Różnowartościowość funkcji.
* Funkcje parzyste, nieparzyste, okresowe.
* Dwumian Newtona.
* Równania i nierówności wykładnicze i logarytmiczne.
* Nierówności trygonometryczne.
* Wzory redukcyjne.
* Przykłady ciągów zdefiniowanych rekurencyjnie.
* Pojęcie granicy ciągu.
* Obliczanie granic ciągów.
* Suma szeregu geometrycznego.
* Pojęcie funkcji ciągłej.
* Pojęcie pochodnej.
* Interpretacja geometryczna i fizyczna pochodnej.
* Obliczanie pochodnych wielomianów i funkcji wymiernych.
* Związek pochodnej z istnieniem ekstremów i z monotonicznością funkcji.
* Zastosowanie pochodnej do rozwiązywania problemów praktycznych.
* Przykłady przekształceń geometrycznych: obrót.
* Twierdzenie o związkach miarowych między odcinkami stycznych i siecznych.
* Wielościany foremne.
* Rzut prostokątny na płaszczyznę.
* Prawdopodobieństwo warunkowe.
* Wzór na prawdopodobieństwo całkowite.
* Niezależność zdarzeń.
* Schemat Bernoullego.
* Twierdzenie o trzech prostych prostopadłych.
aha i mam jeszcze jedno pytanie według tego artykułu NIE może sie pojaic żadne zagadnienie tu
wymienione w zdaniach maturalnych w tym roku ? Posiadam kilka ksiazek przygotowujacych
egzaminujacego do matury i tam polowa jak nie wiekszosc zadan jest z tymi zagadnieniami ? wiec
jak to bedzie tak naprawde bo juz tylko 14 dni a ja dalej nie jestem w 100 % pewny o co tu
chodzi ?
Od 1 września 2007 r. obowiązuje nowa podstawa programowa z matematyki. Różni się ona zakresem
treści od podstawy programowej obowiązującej wcześniej, według której uczona była młodzież,
która przystąpi do egzaminów w roku szkolnym 2008/2009. Mając to na uwadze, dyrektor CKE
ogłosił listę treści, które nie będą sprawdzane na maturze w 2009.
Na egzaminie maturalnym z matematyki na poziomie rozszerzonym nie będą sprawdzane poniższe
treści:
* Twierdzenie o rozkładzie liczby naturalnej na czynniki pierwsze.
* Wzór (a – 1)(1 + a +...+ an−1) = an −1
* Indukcja matematyczna.
* Różnowartościowość funkcji.
* Funkcje parzyste, nieparzyste, okresowe.
* Dwumian Newtona.
* Równania i nierówności wykładnicze i logarytmiczne.
* Nierówności trygonometryczne.
* Wzory redukcyjne.
* Przykłady ciągów zdefiniowanych rekurencyjnie.
* Pojęcie granicy ciągu.
* Obliczanie granic ciągów.
* Suma szeregu geometrycznego.
* Pojęcie funkcji ciągłej.
* Pojęcie pochodnej.
* Interpretacja geometryczna i fizyczna pochodnej.
* Obliczanie pochodnych wielomianów i funkcji wymiernych.
* Związek pochodnej z istnieniem ekstremów i z monotonicznością funkcji.
* Zastosowanie pochodnej do rozwiązywania problemów praktycznych.
* Przykłady przekształceń geometrycznych: obrót.
* Twierdzenie o związkach miarowych między odcinkami stycznych i siecznych.
* Wielościany foremne.
* Rzut prostokątny na płaszczyznę.
* Prawdopodobieństwo warunkowe.
* Wzór na prawdopodobieństwo całkowite.
* Niezależność zdarzeń.
* Schemat Bernoullego.
* Twierdzenie o trzech prostych prostopadłych.
 od 2010 (tej obowiązkowej). Poziom podstawowy (jak
czytałem) będzie miał 20−30 zamkniętych, kilka za 2p oraz kilka 4−6 punktów. Czy poziom
rozszerzony również będzie miał tak samo, czy się nie zmieni?
od 2010 (tej obowiązkowej). Poziom podstawowy (jak
czytałem) będzie miał 20−30 zamkniętych, kilka za 2p oraz kilka 4−6 punktów. Czy poziom
rozszerzony również będzie miał tak samo, czy się nie zmieni?

 chyba kpisz poziom R się nie zmienia no jeszcze może wam
materiał obetną bo zaraz to jeszcze nawet funkcje zabiorą z matury
chyba kpisz poziom R się nie zmienia no jeszcze może wam
materiał obetną bo zaraz to jeszcze nawet funkcje zabiorą z matury
 . Mickej od 2012 (ja się załapię) mają
połowę obciąć materiału
. Mickej od 2012 (ja się załapię) mają
połowę obciąć materiału 


 Nie no żart
Nie no żart 

 Komu przypominasz? Dokończ zadanie już sam. Wpasuj po prostu podane rozwiązania do podanego
przedziału przyjmując odpowiednią wartość k.
Komu przypominasz? Dokończ zadanie już sam. Wpasuj po prostu podane rozwiązania do podanego
przedziału przyjmując odpowiednią wartość k.


 ale czasem pomysłu brakuje albo czegos nie zauwaze...
ale czasem pomysłu brakuje albo czegos nie zauwaze...




 wiec powstanie po odjęciu
wiec powstanie po odjęciu

 czy dobrze wysle
czy dobrze wysle
 ale zostanie jeszcze wykres cos2x... i nie wiem...
ale zostanie jeszcze wykres cos2x... i nie wiem...


 aaaa wiem ze juz zle mam... wykrs po odjeciu sin2x − sinx to bedzie tak jak teraz mam wyzej ..
aaaa wiem ze juz zle mam... wykrs po odjeciu sin2x − sinx to bedzie tak jak teraz mam wyzej ..



 ?
?
 http://www.jogle.pl/wykresy/
http://www.jogle.pl/wykresy/


 a ty napisałes min i nie wiem
a ty napisałes min i nie wiem 

 ale to nie teraz za 30 min to zrobie
ale to nie teraz za 30 min to zrobie
 a wartosc najwieksza kiedy mianownik bedzie najmniejszy
a wartosc najwieksza kiedy mianownik bedzie najmniejszy  dobrze mysle
dobrze mysle
 Δ= −12 − 4 * 2 * −1 = 1+8 = 9
q= 9/ 4*−2 = −9/8
Δ= −12 − 4 * 2 * −1 = 1+8 = 9
q= 9/ 4*−2 = −9/8


 to własnie beda te odpowiednio
najmniejsze i najwieksze
to własnie beda te odpowiednio
najmniejsze i najwieksze
 czy popatrzec ze ramiona paraboli w dol sa...
czy popatrzec ze ramiona paraboli w dol sa... 


 ma być
ma być 
 jak siedzisz do pozna to porobie jakies zadania
jak siedzisz do pozna to porobie jakies zadania  i
jeszcze raz dziekuje za pomoc
i
jeszcze raz dziekuje za pomoc 

 A nie lepiej Pabc= Pabd +Pacd
wzór P= 1/2absinα
Odp:
AD = 12√3/5
A nie lepiej Pabc= Pabd +Pacd
wzór P= 1/2absinα
Odp:
AD = 12√3/5
 ?
?

 tam wczoraj maturzyści machali
tam wczoraj maturzyści machali
 Prawdopodobienśtwo że wygra arsenal moim zdaniem 90 %
Prawdopodobienśtwo że wygra arsenal moim zdaniem 90 %  narazie
narazie
 W sprawie dwusiecznej w trójkącie.
W sprawie dwusiecznej w trójkącie.
 c2 = 42 + 62 − 2*4*6* cos60o
c2 = 28
c = 2√7
c2 = 42 + 62 − 2*4*6* cos60o
c2 = 28
c = 2√7
 pewnie już ją ktoś tutaj widział ale napisze
pewnie już ją ktoś tutaj widział ale napisze  a = b
a2 = ab
a2 − b2 = ab − b2
(a + b )( a − b ) = b( a − b )
a + b = b
2b = b
2 = 1
a = b
a2 = ab
a2 − b2 = ab − b2
(a + b )( a − b ) = b( a − b )
a + b = b
2b = b
2 = 1


 cos367=cos7
cos367=cos7 to z pamięci przerobiłem ale chyba tak ma być
sin19sin7+cos19cos7=cos2=sin88
to z pamięci przerobiłem ale chyba tak ma być
sin19sin7+cos19cos7=cos2=sin88

 bez podpowiedzi
bez podpowiedzi

 Układ równań
a)
(x+2)(y+1) − xy = 0
2y = −2 −x
Układ równań
a)
(x+2)(y+1) − xy = 0
2y = −2 −x

 ma byx x= −
ma byx x= − dla pewności podstaw i sprawdź
dla pewności podstaw i sprawdź 
 DOBRZE
DOBRZE 
 wiec nie pisalem
w rozwiazaniu bo dyza zabawy
wiec nie pisalem
w rozwiazaniu bo dyza zabawy 





 zaczne te zadania rano robic bo jstem juz padniety...
zaczne te zadania rano robic bo jstem juz padniety... 
 są 3 rozwiązania
są 3 rozwiązania



 Zad: Dla jakich wartości parametru "m"
proste y = x +m i y = mx − 4 przecinają się w punkcie należącym
do symetralnej odcinka AB o końcach : A(1,1) B( − 3, 5)
Zad: Dla jakich wartości parametru "m"
proste y = x +m i y = mx − 4 przecinają się w punkcie należącym
do symetralnej odcinka AB o końcach : A(1,1) B( − 3, 5)
 Zastosuj wzór cosinusów"
c2 =( 12a)2 +sa2 − 2*12a*sa*cos(180o− β) =a24 + sa2 +a*sa*cosβ
podobnie:
b2 = (12a)2 + sa2 − 2*12a*sa*cosβ= a24 +sa2 − a*sa *cosβ
dodając stronami obydwa równania otrzymasz:
c2 + b2 = 2sa2 +12a2
dalej juz tylko przekształć i oblicz I saI
Zastosuj wzór cosinusów"
c2 =( 12a)2 +sa2 − 2*12a*sa*cos(180o− β) =a24 + sa2 +a*sa*cosβ
podobnie:
b2 = (12a)2 + sa2 − 2*12a*sa*cosβ= a24 +sa2 − a*sa *cosβ
dodając stronami obydwa równania otrzymasz:
c2 + b2 = 2sa2 +12a2
dalej juz tylko przekształć i oblicz I saI

 Biorąc pod uwagę że w ogóle myślę
Biorąc pod uwagę że w ogóle myślę 


 |1−|x|| ≤3 założenie |x|≥0 − zawsze wiec
|1−x|≤3 1−x ≥0
x≤1
|1−x| ≤ 3 ⋀ |1−x| ≥ −3
1−x ≤ 3 1−x ≥ −3
−x ≤ 2 −x ≥−4
x ≥ −2 x ≤ 4
x∊ <−2 ; 4>
|1−|x|| ≤3 założenie |x|≥0 − zawsze wiec
|1−x|≤3 1−x ≥0
x≤1
|1−x| ≤ 3 ⋀ |1−x| ≥ −3
1−x ≤ 3 1−x ≥ −3
−x ≤ 2 −x ≥−4
x ≥ −2 x ≤ 4
x∊ <−2 ; 4>  Zgadza się
Zgadza się 






 Jeżeli pochodna to]
3t2 + 4t +5 = 0
6t + 4 = 0
6t = −4
Jeżeli pochodna to]
3t2 + 4t +5 = 0
6t + 4 = 0
6t = −4
 POmoże mi ktos z tymi końcówkami zadań
POmoże mi ktos z tymi końcówkami zadań 

 czyli mam źle
czyli mam źle 
 bo jak sprawdziłem przedział <−2 ; 4> to sie zgadzało...
bo jak sprawdziłem przedział <−2 ; 4> to sie zgadzało... 
 chodzi mi o pierwszą wart. bezwzględna
chodzi mi o pierwszą wart. bezwzględna 
 jak potrafie
jak potrafie 


 bo sie staram jak moge ...
bo sie staram jak moge ...  a jesli zle to powiedzcie
gdzie jest błąd...
a jesli zle to powiedzcie
gdzie jest błąd... 



 popatrzcie na moje rozwiazania czy robie dobrze prosze...
popatrzcie na moje rozwiazania czy robie dobrze prosze... 
 bo pierw. dwukrotnym
jest "2" a trzykrotnym jest "−2"
bo pierw. dwukrotnym
jest "2" a trzykrotnym jest "−2" 
 hmmm czyli wykres mam zle...
hmmm czyli wykres mam zle... własnie dochodze do tego co napisałes...
własnie dochodze do tego co napisałes... 
 juz wiem
juz wiem  2 jest podwójnym a −2 pojedynczym − znaki mi sie pomyliły jak
patrzyłem na twoje rozwiazanie
2 jest podwójnym a −2 pojedynczym − znaki mi sie pomyliły jak
patrzyłem na twoje rozwiazanie  CZYLI MAM DOBRZE
CZYLI MAM DOBRZE  jupi
jupi 




 sprawdzic czy wynik jest ≥0 czy co....
sprawdzic czy wynik jest ≥0 czy co.... 

 z rozwiązaniem
https://matematykaszkolna.pl/strona/263.html
z rozwiązaniem
https://matematykaszkolna.pl/strona/263.html
 juz licze dalej
juz licze dalej 




 przy ciągach się nie rysuje
przy ciągach się nie rysuje nie możesz z nierówności przechodzić na równość
przyrównując coś do zera
nie możesz z nierówności przechodzić na równość
przyrównując coś do zera są 2 sposoby rozwiązywania takich zadań książkowy ten który
zaproponował Bogdan albo taki bardziej nie książkowy jak ci podawałem tylko przy moim gdy coś
opuszczasz to zawsze uzasadniaj dlaczego tak robisz:0
są 2 sposoby rozwiązywania takich zadań książkowy ten który
zaproponował Bogdan albo taki bardziej nie książkowy jak ci podawałem tylko przy moim gdy coś
opuszczasz to zawsze uzasadniaj dlaczego tak robisz:0
 nie łapie
nie łapie 
 pamiętam że jakiś czas temu było parę zadanek tego typu na forum
poszukaj
pamiętam że jakiś czas temu było parę zadanek tego typu na forum
poszukaj ładnie rozwiązane były
ładnie rozwiązane były jeśli nie znajdziesz to ja rozhukam to zadanko
jeśli nie znajdziesz to ja rozhukam to zadanko



 Nie moge do tego dojsc
Nie moge do tego dojsc 
 teraz juz wiem
teraz juz wiem  DZIĘKUJE
DZIĘKUJE  wynik to −4(n+3)(n+2)
wynik to −4(n+3)(n+2)
 poprawimy:
an= U{(n+2)!*n}{5n
poprawimy:
an= U{(n+2)!*n}{5n




 Majówkę zaliczyłam
Majówkę zaliczyłam  ...... teraz patrzę jak się uwijasz
...... teraz patrzę jak się uwijasz  Cześć pracy
Cześć pracy


 cienko u mnie
z taką teorią ale wykazać bym wykazał
cienko u mnie
z taką teorią ale wykazać bym wykazał

 ja np nie rozumiem w rozwiązaniu Bogdana dlaczego
ja np nie rozumiem w rozwiązaniu Bogdana dlaczego
 Zadanie z kwadratem :
d= a√2
r= 1/2a√2
1/2a√2= r / 1/2
a√2= r/2
a=r√2
a1(czarna kropka) =r√2 a q= √2/2
czyli P= a2 = 2r2 , q2= (√2/2)2 = 1/2
gdzie |q|< 1
a1
S= −−−−−− = 2r2 * 2/1 = 4r2
1− q
Zadanie z kwadratem :
d= a√2
r= 1/2a√2
1/2a√2= r / 1/2
a√2= r/2
a=r√2
a1(czarna kropka) =r√2 a q= √2/2
czyli P= a2 = 2r2 , q2= (√2/2)2 = 1/2
gdzie |q|< 1
a1
S= −−−−−− = 2r2 * 2/1 = 4r2
1− q