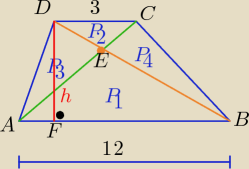
Oblicz pola trójąktów w trapezie. Genevive: W trapezie ABCD podstawy mają długość |AB|= 12 cm, |DC|= 3 cm. Wysokość trapezu jest równa 10 cm, a punkt E jest punktem przecięcia się przekątnych trapezu. Oblicz pola trójkątów ABE i CDE. Prosze o pomoc

Basiek: z podobieństwa trójkątów ABE, DCE k=12/3= 4 h₁=4h₂ =>H= h₁+h₂=5h₂= 10cm=> h₂=2cm , h₁=8cm A pola... to już chyba policzysz

Eta:

	12
ΔABE ~ ΔCDE w skali k=		=4
	3

ze wzoru:

	12+3
P(tr) = (k+1)2*P2 P(tr)=		*10 = 75
	2

zatem: 75=(4+1)²*P₂ ⇒ P₂= P(ΔCDE)= 3 P(ΔABE)= P₁= k²*P₂= 16*3= 48 oraz P₃=P₄= k*P₂= 4*3= 12 spr. P(tr)= P₁+P₂+P₃+P₄= 48+3+12+12= 75 , czyli ok

Eta: Dla Basiek .... Ja wykorzystałam mój ulubiony wzorek

Genevive: Dzięki