pole powierzchni Kwachu: jak mam w zadaniu polecenie, by obliczyć pole obszaru znajdującego się między funkcjami f(x), g(x)... to wynik zawsze musi wyjść na plusie. Ale czasami, chyba po złych przekształceniach przy całce, wyniki czasami wychodzą ujemne. Zazwyczaj stosuję wzór na zapisanie całki taki że _a∫^b g(x)−f(x) ponieważ taki ogólny gdzieś ujrzałem i zapamiętałem. i teraz, żeby mieć wynik na plusie, chyba powinienem brac zawszę tą prosta, parabole czy inną funkcję która ma wieksze wartości od tej drugiej funkcji nie patrząc na ten wzór _a∫^b g(x)−f(x) tylko żeby za g(x) podstawiać funkcję większą a f(x) to funkcja pod g(x). Dobrze myślę?

Krzysiek: tak, tylko g(x) ma być na całym przedziale [a,b] nad funkcją f(x)

Kwachu: wtedy jak są jakieś "załamania" wtedy rozumiem żeby podzielić na 2 obszary d1 i d2?

Kwachu: jak mam f(x)=x² + 4x i g(x)=x+4 to czy; _a∫^b x+4dx + _a∫^b x² + 4xdx = _a∫^b −x² −3x + 4dx?

Kwachu: tam między 1 a 2 całkom ma być −

Krzysiek: tak, i na przedziale: [−4,1]

Kwachu: Krzysiek widze że ty i Basia ogarniacie te tematy mam nadzieję że nie będziecie źli jak będę dawał non stop jakieś oczywiste pytania. jutro mam koło od którego zależy czy będę zwolniony z egzaminu i zależy mi, żeby poznać każdą oczywistość

Krzysiek: Więcej ludzi zna się na tego typu rzeczach pomocny jest też Wolfram (http://www.wolframalpha.com/ ) wpisujesz całkę i otrzymujesz wynik i krok po kroku rozwiązanie (nie zawsze najłatwiejsze)

Kwachu: znam te "kalkulator" ale właśnie nie zawsze do końca rozumiem dlaczego tak skoro można było to zrobic tak. A jasne dla mnie jest raczej to że ty czy ktokolwiek inny bedzie wolał zrobić to jak najprościej a taki jak najszybciej

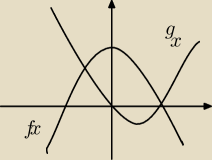
Kwachu: jak mam takie 2 funkcje f(x)=4−x² i g(x)=x² −2x to całka będzie wyglądała tak: ₋₁∫² f(x) − g(x) ?

Krzysiek: tak

Kwachu: nadal do tego wykresu

	−2x3
−1∫2 4−x2 − x2 + 2x dx= −1∫2 −2x2 + 2x + 4dx= [		+x2 + 4x −1] 2 =
	3

	31
		?
	3

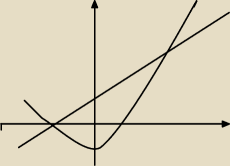
Kwachu: Parabola to f(x) a prosta to g(x). całkę zapisać ∫g(x)−f(x) bo funkcja g jest nad funkcja f prawda?

Krzysiek: powinno wyjść 9 co do tego wykresu: tak

Kwachu: czyli gdzieś się machnąłem przy podstawianiu wartości za x czy mam zle całkę w ogóle policzoną?

Krzysiek: całkę nieoznaczoną dobrze policzyleś

Asyy:

20		7		27
	− (−		) =		=9 [j2]
3		3		3

Kwachu: zbieżność całek mam ₀∫^∞ xe^−x2 dx = _a→0lim_{b→∞ 0}∫^∞ xe^−x2 dx 1) obliczam całkę nieoznaczoną:

	1		1		1
∫xe−x2 dx = −∫		en dn= −		en=−		e−x2 n=−x2
	2		2		2

2) podstawiam do całki oznaczonej a i b

	1		1
a∫b xe−x2 dx = −		e−b2 +		e−a2
	2		2

3)obliczam zbieżność _a→0lim_{b→∞ 0}∫^∞ xe^−x2 dx= ∞ czy to jest dobrze?

Krzysiek: liczysz tylko granicę dla b→∞, przecież jak wstawisz 0 to nie masz symbolu nieoznaczonego ∫₀^∞ xe^−x2 dx =lim b→∞ −1/2 e^−x2 |₀^b =...

Kwachu: czyli jak za x podstawie ∞ a potem odejmę od tego −1/2 to mam ∞+1/2 =∞ o to chodzi?

Krzysiek: tylko, że: lim b→∞ e^−b2 =0

Kwachu: ok łapie. bażda liczba podniesiona do ∞ = 0 i wynik bedzie 1/2 granice miałem na początku roku i już trochę zapomniałem

Krzysiek: źle.. nie każda liczba podniesiona do ∞ to 0...

	1
tylko: e−b2 =
	eb2

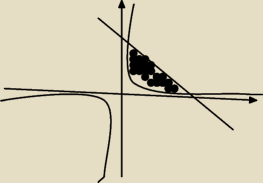
Kwachu: mam tu wykres dla y=6/x i y=−x+7 skoro prosta jest nad y=6/x to całke powinienem zapisac ∫−x+7−6/x dx a na zajęciach zapisaliśmy ∫6/x + x −7dx. Ja się pomyliłem teraz czy na zajęciach ktoś źle podstawił za f(x) i g(x)?