Figury i przekształcenia Help!!! xD JJ: Odległośćpunktu A=(5,6) od punktu B położonego na osi odciętych jest równa 10. Wyznacz współrzędne punktu B.

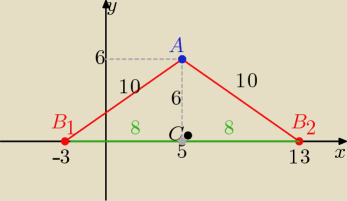
Eta: B₁(−3,0) , B₂(13,0)

123: A = (5, 6) B = (x, 0) |AB| = 10 |AB| = √(x − 5)² + (0 − 6)² 10 = √(x − 5)² + (0 − 6)² 100 = (x − 5)² + 6² 100 = x² − 10x + 25 + 36 100 = x² − 10x + 61 x² − 10x − 39 = 0 Δ_x = (−10)² − 4*1*(−39) Δ_x = 100 + 156 Δ_x = = 256 √Δ_x = 16

	10 − 16		−6
x1 =		=		= −3
	2		2

	10 + 16		26
x2 =		=		= 13
	2		2

Dla x₁ = −3 B = (−3, 0) Dla x₂ = 13 B(13, 0)

123: Tak. Eta bardzo ładnie zastosowała graficzną definicję wartości bezwzględnej jako odległości. Tak też można ale na maturze nie wiem czy by tak uznali

JJ: Wielkie dzięki. Jeszcze mam kilka zadań do rozwiązania pomożecie?

Eta: Czemu niby by mieli nie uznać?

123: No chodzi mi o to, że np jak są zadania polegające na obliczeniu a on dał by rysunek to nie wiem czy tak można bo równie dobrze mógłby w analitycznej lecieć po kratkach i odczytać wierzchołki rombu, które trzeba wyliczyć

123: @ JJ Możesz dać te zadania to pomożemy

LBJ: Proste o równaniach x−3=0, 2x+y−16=0, y−2=0 wyznaczają trójkąt ABC. a)Oblicz współrzędne wierzchołków trójkąta ABC b)Napisz równanie okręgu opisanego na trójkącie ABC c)Oblicz pole koła opisanego na tym trójkącie Z góry dziękuje

123: a) Liczysz takie układy równań (są to punkty przecięcia się prostych, które są kolejnymi wierzchołkami trójkąta:

⎧	x − 3 = 0
⎩	2x + y − 16 = 0

⎧	x − 3 = 0
⎩	y − 2 = 0

⎧	2x + y − 16 = 0
⎩	y − 2 = 0

b) Liczysz środki dowolnych dwóch boków i wyprowadzasz równania 2 prostych prostopadłych przechodzących kolejno przez te 2 punkty. Potem bierzesz ich część wspólną (układ równań) i masz środek okręgu. c) Liczysz ze wzoru na odległość między 2 punktami odległość pomiędzy 1 z dowolnych wierzchołków a dopiero co obliczonym wierzchołkiem okręgu opisanego. Potem liczysz normalnie pole koła (πr²).

JJ: Środek symetrii prostokąta ABCD ma współrzędne S=(5¹₂),5 a jeden z boków zawiera się w prostej o równaniu 4x+3y−12=0. Wiedząc, że (wektor) SA=(−5¹₂),−1, wyznacz: a)współrzędne wierzchołków prostokąta ABCD b)nierówność opisującą koło opisane na prostokącie ABCD

123: a) Liczysz A:

	11
SA = [xa −		, ya − 5]
	2

	11		11
[−		, −1] = [xa −		, ya − 5]
	2		2

	11		11
xa −		= −		⇒ xa = 0
	2		2

y_a − 5 = −1 ⇒ y_a = 4 A(0, 4) b) Liczę C:

	11		xc + 0		yc + 4
(		, 5)= (		,		)
	2		2		2

11		xc + 0
	=		⇒ xc = 11
2		2

	yc + 4
5 =		⇒ 10 = yc + 4 ⇒ yc = 6
	2

C(11, 6) Nie mam już siły dalej liczyć wybacz...

Eta: Zjedz

JJ: Spoko xD Tak dużo już wiem dzięki Tobie

123: Podpowiem tylko tak:

	−4x + 12
Punkt B ma współrzędne B(x,		i liczysz współrzędne wektora AB potem BC i robisz
	3

tak: AB o BC = 0 ⇔ x_a*x_b + y_a*y_b = 0 Punkt D wylicz tak: 1. Wyznacz prostą przechodzącą przez punkt S i dopiero co wyliczony B. Punkt D spełnia równanie nowo wyznaczonej prostej podobnie jak poprzednio punkt B i znowu wylicz wektory AD i DC i zastosuj: AD o DC = 0 ⇔ x_a*x_d + y_a*y_d = 0

123: Jest to tzw. iloczyn skalarny, a ponieważ w trójkącie wszystkie kąty są proste dlatego iloczyn 2 wektorów tworzących kąt prosty jest zawsze równy 0.