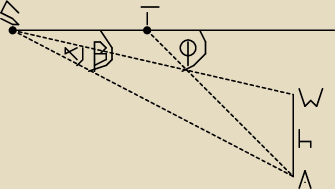
Zero pomysłów... o.O daveustro: Kiedy samolot lecący ze stałą prędkością znalazł się w punkcie S, pilot zmierzył kąt widzenia wieży α oraz depresję jej podnóża β (α<β). Po przebyciu trasy ST długości 800m ponownie zmierzył depresję podnóża wieży: φ (φ>β). Zakładając, że tor lotu samolotu i wieża leżą w jednej płaszczyźnie, wyznacz wysokość h wieży AW. Nawet nie wiem jak zacząć... Co trzeba zauważyć, jak to zrobić? Mógłby ktoś rzucić jakimś pomysłem, rozwiązać pozdr

tim: Mogę wkleić rozw.. jeżeli nikt nie wpadnie. [Ja tylko skopiuje]]

@Basia: kąt STA = 180−fi kąt SAT = 180−β − (180−fi) = fi − β z tw.sinusów

ST		SA		SA
	=		=
sin(fi−β)		sin(180−fi)		sin(fi)

	800*sin(fi)
SA =
	sin(fi−β)

ST		AT
	=
sin(fi−β)		sin(β)

	800*sinβ)
AT =
	sin(fi−β)

przedłuż AW punkt przecięcia ST i przedł.AW nazwijmy B

	AB
sin(fi) =
	AT

z tego liczysz AB

	TB
cos(fi) =
	AT

z tego liczysz TB z tr.SBW masz

	BW		BW
sin(β−α) =		=
	SB		ST+TB

z tego liczysz BW h = AB−BW

tim: Basiu, mogę wkleić? Porównasz..

@Basia: Jasne, że możesz.

tim: http://img2.vpx.pl/up/20090426/przechwytywanie.gif

@Basia: Nie rozumiem 2 kroku tego rozwiązania. Dlaczego α+β+STA +SAT = 180 ? Zgodnie z rysunkiem daveustro β+STA+SAT=180 A wydaje mi się, że rysunek daveustro jest prawidłowy. Wydaje mi się bo nie bardzo wiem co to jest depresja. A już wiem. daveustro źle zaznaczył kąt α. α to kąt BSW. Czyli to wklejone przez Ciebie rozwiązanie jest prawidłowe.

@Basia: Ale z tego by wynikało, że depresja β to kąt ASW ? Jest tak ? Bo jeśli nie, to to wklejone też nie jest poprawne

@Basia: No to mi się nie zgadza. Wg mnie α = BSW β = ASW fi = ATB wtedy STA = 180−fi SAT = 180−β−(180−fi) = fi−β

ST		SA		AT
	=		=
sin(fi−β)		sin(180−fi)		sinβ

z tego liczę SA i AT

	AB
sin(fi) =		z tr.TBA
	AT

	TB
cos(fi) =
	AT

z tego liczł AB i TB z tr.SBW

	BW		BW
tgα =		=
	SB		800+TB

z tego liczę BW h = AB−BW ale może mylę się co do tych katów

daveustro: O nice właśnie zjadłem obiad, już czytam, co mi tu napisaliście, ale z góry dzięki

@Basia: Błąd: β=ASB tak to rozumiem, ale może źle.

daveustro: już piszę te kąty: α = kąt ASW β = kąt AST (przyjmując, że B, to punkt przecięcia się przedłużeń ST i AW, to) φ = ATB

@Basia: dlaczego α=ASW ? wg.mnie α=BSW przecież to kąt pod jakim pilot z poziomu SB widzi wierzchołek wieży W co do β zgadzam się z Tobą, ale w rozwiązaniu wklejonym przez Tima β=ASW i tego w tym rozwiązaniu nie rozumiem

daveustro: no w sumie nie wiem, dlaczego akurat tam jest α tak mam na rysunq w zadaniu na te nazwy depresji osobiście wiele nie patrze, bo ładnie to właśnie na tym rysunq przedstawione

daveustro: http://img23.imageshack.us/img23/8331/zad6add.jpg

@Basia: Do tego rysunku jest to pierwsze rozwiązanie jakie napisałam, ale ja się z tym rysunkiem nie zgadzam, pod warunkiem, że poprawnie napisałeś treść.

tim: To jest zad. z egz. maturalnego [zaraz ci dam lnk]

tim: http://www.edz.win.pl/tgronek/matematyka.php?get=Maturaprbnan14PR.pdf

daveustro: Treść też ctrl+c −> ctrl+v Ale dzięki, idea jest, więc git pozdr

@Basia: A nie, jednak dobrze. kąt widzenia wieży, a nie jej wierzchołka. Czyli to pierwsze rozwiązanie jest dobre. Nie rozumiem w takim razie rozwiązania wklejonego przez Tima

daveustro: właśnie tim, masz może wyniki do niego

tim: Nie

daveustro:

@Basia: No to w żaden sposób w tr.STA nie będzie tak jak w tym wklejonym rozwiązaniu. Będzie tak jak napisałam.

daveustro: a do tego jakiś pomysł? kiedyś była jakaś zagadka z kelnerką, że się złotówka zgubiła, czy coś takiego, ale to było proste, bo kolejność rozwiązań (o ile dobrze pamiętam) była istotna a tutaj? http://alfaiomega.matematyki.w.interia.pl/grafika/ciekawostki/jakto.jpg

tim: To jest banalne Sprawdź sobie pochyłość

daveustro: ale jak... przecież podstawa ta sama długość, druga przyprostokątna to samo, więc z pola w trójkącie prostokątnym to samo wychodzi... no i nie wiem o co z tą pochyłością?

tim: No ok są dwa trójkąty, ale! mają inną pochyłą przyłóż sobie linijkę i porównaj

daveustro: no to wracam do trójkąta pitagoryjskiego: a² + b² = (przecież) c² więc ta przeciwprostokątna też będzie równa... czy jednak nie? (przecież nie bd linijką po monitorze jeździł )

tim: Nie chodzi o długość, tylko ta przyprtokątna NIE JEST prosta. przyłóż linijkę.

@Basia: pionowa przyprostokątna zielonego nie jest identyczna; stąd

daveustro: no i zgłupiałem... przyprostokątne (przecież to widać po tych linijkach) są obie proste... pionowa przyprostokątna zielonego też jest taka sama (bo po 2 jednostki) więc dalej nie wiem ale przyznacie, że ciekawe

tim: Co?

tim: MI CHODZI O PRZECIWPROSTOKĄTNE.. NAPRAWDĘ PRZYŁÓŻ!

daveustro: no przyłożyłem i dalej nie wiem (nie zauważam tam tej nieprostoliniowości) ale dobra, uwierzę Ci tim na słowo to teraz na odskok od rysunków itp. http://www.edz.win.pl/tgronek/matematyka.php?get=Wyr.wymiernedlaA2.pdf

tim: PRZECIWPROSTOKĄTNE ZIELONEGO I CZERWONEGO TRÓJKĄTA SĄ RÓŻNE (PADAJĄ POD INNYM KĄTEM, POLICZ SOBIE NP. COS, CZY COŚ) PRZEZ TO JAK CZERWONA POSZŁA DO GÓRY, ZAJMUJE TAM WIĘCEJ MIEJSCA. SIN CZERWONEGO = 3/8 SIN ZIELONEGO = 2/5 ICH PRZECIWPROSTOKĄTNE PADAJĄ POD INNYM KATEM!

tim: Uf.

daveustro:

tim: ROZUMIESZ?

tim: Skoro kąty są inne, to zmieniając kąty, zmieniasz pole, dlatego ten jeden tam jest pusty

daveustro: no tak mniej więcej, +/− ale tam chyba zamiast SIN czerwonego i zielonego, to chyba miał być TG, tak?

@Basia: Tim jeżeli kat się zmienił a przeciwprostokatna nie to musiała zmienić się przyprostokatna. Pionowa zielonego nie ma na górnym rysunku 2 jednostek. I tyle.

@Basia: Na dolnym zresztą też nie musi. Bo kto wam powiedział, że to szerokie = dwa małe ?

daveustro: a nie? przecież jak te grubszą podzielisz na dwie równe części, to będą 2 jednostki i będzie pasowało... w sensie nie pasowało

@Basia: No właśnie w tym rzecz, że nie muszą. Pomiar nawet z dokładnością do 0,5 mm. to za mało, żeby mieć pewność. A różnica kątów już da się zauważyć.

tim: @Basiu, więc co w końcu?

daveustro: w każdym bądź razie, wracając do zadania z początku, jak Wam to powychodziło? bo mi dość dziwny wynik wyszedł, a nie mam tego jak sprawdzić

daveustro: Na powierzchni kuli narysowano okrąg wielki (to znaczy mający środek w środku kuli) i styczny do niego okrąg o połowę krótszy. Kąt, jaki tworzą płaszczyzny zawierające te okręgi ma miarę: A) π/6 B) π/5 C) π/4 D) π/3 Zadanie pasuje do tego wczorajszego tematu: zero pomysłów... o.O O co w tym w ogóle chodzi?

tim: Tzn wiem, że odp D (z arkusza), ale czemu już nie.. To musi Basia, albo ktoś ze "starszyzny"

daveustro: Wszystkie arkusze, z których robię zadania już znasz? respect Do tego akurat mam też te odpowiedzi, ale właśnie nie rozumiem w ogóle treści ;\ To prośba do Basi, albo kogoś ze "starszyzny" Mógłby ktoś wytłumaczyć?

tim: [Pozdrowienia dla google.pl] Ja też średnio, więc się nie wypowiadam.

daveustro: No tak, wujek google wszystko zna

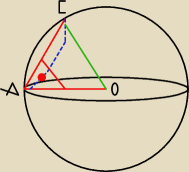
@Basia: czerwona kropka − szukany kąt R − promień kuli Wszystkie punkty niebieskiego okręgu leżą na powierzchni kuli, stąd OA = OC = R AC jest średnicą tego małego okręgu (o połowę krótszego) czyli AC = połowie średnicy koła wielkiego kuli czyli AC = R tr. AOC jest równoboczny ⇒ α=60 = ^π₃

daveustro: To jak "starszyzno"? Uda się? plz help

daveustro:

@Basia: Ta niebieska przerywana linia to powinna być elipsa. Bo tak widzimy w rzucie okrąg. @Jakubie ! Dlaczego nie można narysować elipsy z ukośnymi średnicami ?

daveustro: Noo, dzięki Basia Zrozumiałem, aczkolwiek sam bym na to chyba nie wpadł... Także dzięki