Funkcja Ala:

	x
Dana jest funkcja f(x)=		, x ∈R−{−2,2}. Wykaz ze zbiorem wartosci jest zbior
	4−x2

liczb rzeczywistych

dpelczar: Jesli sie myle to mnie uswiadomcie... ale uwazam ze Z_w ∈(−∞ , 0)

tim: A np. x = − 100 ?

tim: dpelczar spr.

Mickej : zbioru wartości się nie sprawdza podstawiając pod x tylko pod y i najprościej w tym przypadku wyznaczyć x=... albo naszkicować wykres

dpelczar: marysowalem wykres i wyszlo mi to co napisalem... ze Z_w ∈ (−∞ , 0) ale moze zly wykres mam

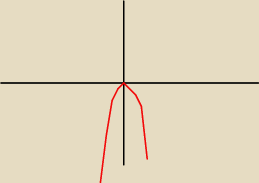
dpelczar: w przyblizeniu cos takiego... dobrze

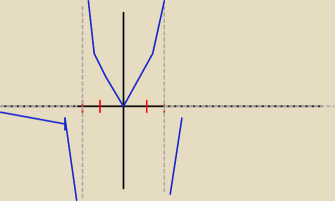
tim: Mickej.. Naszkicować wykres?

tim: Mi tak wyszło

tim: Jednak przy x ujemnych (0,2) to będzie w dól

Mickej : bardzo prosto podstawić 1 i widać

	1
f(1)=		więc przykro mi ale wykres jest zły drugie ramie to prawe ma iść do góry i
	3

zriorem faktycznie jest R

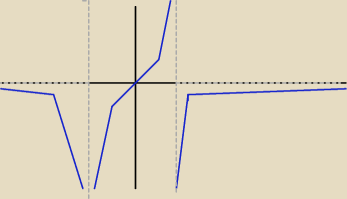
tim: Może tak?

dpelczar: a jak do tego doszedles wiem ze mam juz zle ale wymyslilem cos takiego: zeby f(x) > 0 to x<0 i 4 − x² < 0 x>0 i 4 − x² > 0 taki uklad rownan... prosze poweidz ze przynajmniej to prawdziwie i dobrze napisalem...

dpelczar: ale jak narysowaliscie wykrasy... jaki przeksztalcenia

Mickej : wykres masz nadal zły tim

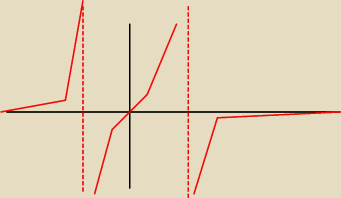
tim: Jeżeli źle toże mógłbyś mnie oświecić Mickej?

dpelczar: tim jak do tego doszedles ? jak zauwazyls

tim: Co?

dpelczar: no ze takie wykresy... podzieliles sobie na przedzialy np. (−∞ ; −2) (−2 ; 2) (2 ; +∞) czy jak inaczej

Michał Szczotka:): można ale ten wykres to jest taka dzika sprawa jak taki widzę to liczę granice sobie i ten ostatni wykres tima też nie jest jeszcze poprawny bo skrajne ramiona mają być na odwrót

xpt: dpelczar & tim − w poleceniu pisze, że D=ℝ\{−2,2} więc wykres tej funkcji powinien zawierać się w tym przedziale. Nikt nie pyt, np.a jak ma się funkcja dla x=3. Michał Szczotka: chodzi Ci o to, gdy x→∞ i x→−∞ ? dpelczar: dla x∈{−2,2} funkcja traci sens liczbowy wiec dlatego tim podzielił wykres tymi 2ma punktami.

xpt: A właśnie − dpelczar − co masz na myśli pisząc "Z_w" ? Bo nie kojarzę takiego oznaczenia.

dpelczar: Z_w −−−−> zbior rozwiązan

Michał Szczotka:): o mamy kolejną osobę która włączyła się do dyskusji xpt zauważ że dziedzina nie jest określona x ∈R−(−2;2) tylko x ∈R−{−2,2} a to całkiem 2 różne rzeczy w przypadku jaki podała Ala dziedziną jest zbiór liczb rzeczywistych bez 2 i −2

xpt: Faktycznie − wydawało mi się, że tam są okrągłe nawiasy, nie klamrowe. W trzeba obliczyć granice lewo i prawostronne dla x→±2, a następnie sprawdzić czy funkcja jest ciągła na przedziale (−2,2). Pytanie tylko czy Ala nie umie obliczyć tego zadania, czy po prostu nie miała pomysłu jak się za to zabrać?

Ala: ha ha, teraz juz umie, ale gorzej bylo z pomyslem

xpt: dpelczar − tak się zastanawiałem, bo ja się przyzwyczaiłem, ze zriór liczb całkowitych oznaczam "ℤ" Od razu uprzedzam ewentualne pytania − znak "ℂ" jest zarezerwowany dla zbioru liczb zespolonych.

xpt: Ala: Czyli zadanie można uważać za rozwiązane ?

Michał Szczotka:): no teraz się zgadzamy

Ala: uwazam ze tak

Michał Szczotka:): liczby zespolone to nie w liceum xpt

xpt: Michale − wiem, dlatego w liceum stosuje się "C" jako oznaczenie liczb całkowitych. Nie wiedziałem po prostu o co chodziło z zapisem Z_w bo w liceum korzystałem z D⁻¹

Michał Szczotka:): no wiem ale ja wole napisać zbiór wartości albo przeciw dziedzina bo wtedy nikt sie nie doczepi

dpelczar: Przeciw dziedzina o tym to dopiero na studiach slyszalem...

tim: Przeciwdziedzina to odwrotne D