
 Nic nie rozumiem !
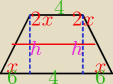
1.W trapezie równoramiennym kąty przy krótszej podstawie maja miare dwa razy dłuższą niż kąty
przy dłuższej podstawie . Dłuższa z podstaw ma długość 16 cm a odcinek łączący srodki ramion
10 cm . Oblicz pole i obwód tego trapezu .
2. Wyznacz pole koła wpisanego w romb o kącie ostrym α i boku a
3.Wyznacz promien okregu wpisnaego w romb o polu P i kacie ostrym α
4.Z punktu P poprowadzona styczna do okregu w punkcie A o sieczna przecinajaca okrag w punktach
B i C Oblicz pola trojkata ABC jezeli:
a) IAPI = 6, IPBI=34IPCI oraz sin ∠APB = √33
b) IPAI=8 IPCI =4 oraz cos∠APB =34
Nic nie rozumiem !
1.W trapezie równoramiennym kąty przy krótszej podstawie maja miare dwa razy dłuższą niż kąty
przy dłuższej podstawie . Dłuższa z podstaw ma długość 16 cm a odcinek łączący srodki ramion
10 cm . Oblicz pole i obwód tego trapezu .
2. Wyznacz pole koła wpisanego w romb o kącie ostrym α i boku a
3.Wyznacz promien okregu wpisnaego w romb o polu P i kacie ostrym α
4.Z punktu P poprowadzona styczna do okregu w punkcie A o sieczna przecinajaca okrag w punktach
B i C Oblicz pola trojkata ABC jezeli:
a) IAPI = 6, IPBI=34IPCI oraz sin ∠APB = √33
b) IPAI=8 IPCI =4 oraz cos∠APB =34


| a+b | ||
1. odcinek łączący środki ramion trapezu liczy się ze wzoru d= | , gdzie d to własnie | |
| 2 |
 b−długość krótszej podstawy a − długość dłuższej a=16cm
b−długość krótszej podstawy a − długość dłuższej a=16cm
| 16+b | ||
10= | ||
| 2 |
| 6 | ||
cos60= | ||
| c |
| 1 | ||
cos60= | ||
| 2 |
| 1 | 6 | ||
= | |||
| 2 | c |
| h | h | |||
h liczysz też z funkcji np tg tg60= | tg60=√3 √3= | |||
| 6 | 6 |
 resztę zrobię
po meczu
resztę zrobię
po meczu 

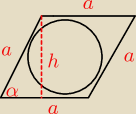 2r=h
2r=h
| h | ||
sinα= | ||*a
| |
| a |
| a*sinα | ||
r= | ||
| 2 |
| πa2sin2α | ||
Pk= | ||
| 4 |

| P | ||
a= | ||
| 2r |
| h | ||
sinα= | ||
| a |
| 2r | ||
sinα= | ||
| a |
| P | ||
a= | ||
| 2r |
| P | |
*sinα=2r||*2r
| |
| 2r |
| P*sinα | ||
r2= | ||
| 4 |
| √P*sinα | ||
r= | ||
| 2 |

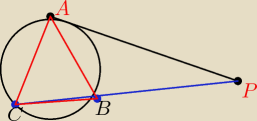 ∡APB bedę oznaczał jako α, żeby było wygodniej
∡APB bedę oznaczał jako α, żeby było wygodniej 
| √3 | ||
sin∡APB=sinα= | ||
| 3 |
| 3 | ||
|PB|= | |PC|
| |
| 4 |
| 3 | ||
62= | |PC|*|PC|
| |
| 4 |
| 3 | ||
36= | *|PC|2
| |
| 4 |
| 4 | ||
|PC|2=36* | ||
| 3 |
| 3 | ||
|PB|= | |PC|
| |
| 4 |
| 3 | ||
|PB|= | *4√3=3√3
| |
| 4 |
| 1 | √3 | |||
PAPC= | *6*4√3* | =12
| ||
| 2 | 3 |
| 1 | √3 | |||
PAPB= | *6*3√3* | =9
| ||
| 2 | 3 |

 kimkolwiek jesteś
kimkolwiek jesteś  a 4 zadanie :
Z punktu P poprowadzona styczna do okregu w punkcie A i sieczna przecinajaca okrag w punktach B
i C Oblicz pole trojkata ABC jezeli:
a 4 zadanie :
Z punktu P poprowadzona styczna do okregu w punkcie A i sieczna przecinajaca okrag w punktach B
i C Oblicz pole trojkata ABC jezeli:
| 3 | √3 | |||
a) IAPI = 6, IPBI= | IPCI , oraz sin ∠APB = | |||
| 4 | 3 |
| 3 | ||
b) IPAI=8 , IPCI =4 , oraz cos∠APB = | ||
| 4 |

 TO JESZCZE RAZ DZIEKUJE i podziwiam ze chciało ci sie siedziec z tym prawie do
2 w nocy
TO JESZCZE RAZ DZIEKUJE i podziwiam ze chciało ci sie siedziec z tym prawie do
2 w nocy 