Bardzo bardzo pilne:(( pomocy !!! Każde rozwiązane zadanie sie liczy !! Karolina!!: 1. Kat wewnętrzny dziewięciokąta foremnego ma miarę 2. Jesli jeden z boków trójkąta jest średnicą okręgu opisanego na tym trójkącie, to trójkąt ten jest 3. W trójkącie równoramiennym kąt przy podstawie ma miarę 6 razy mniejszą od miary kąta między ramionami. Miara kąta między ramionami wynosi 4.Środek okręgu opisanego na trójkącie, to punkt, w którym przecinają się a) dwusieczne kątów trójkąta b)symetralne boków trójkąta c)wysokość trójkąta d)środkowe trójkąta 5. Kat wspisane oparty na tym łuku co kąt środkowy o mierze 28 stopni ma miarę 6. W której ćwiartce układu współrzędnych lezy środek odpinka AB , gdy a=(−17, 3 ) oraz b=(7,19)? 7. Pole rombu jest równe 25 , a kąt ostry ma miarę 30 stopni. Długośc boku tego rombu jest równa 8.Boki trójkąta ABC mają długośc 3 cm, 7cm i 6cm. Obwód trójkąta EFG podobnego do trójkąta ABC jest równa 40cm. Najdłuzszy bok trójkąta EFG jest równy 9. Drabinę o długości 5 m oparto o ścianę budynku na wysokości 2,5m. Miara kąta jaki tworzy drabina z nziemią jest r ówna 10. Wtrójkącie prostokątnym jedna z przyprostokątnych jest równa 8 cm , a przeciwprostokątna 10 cm. A) oblicz długość okręgu opisanego na tym trójkącie. b) Oblicz promień okręgu wpisanegow ten trójkąt.

Karolina!!: a i była bym wdzięczna za obliczenia:((

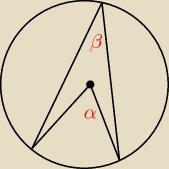
Maadzia : α=2β zatem 28=2β β=14

Maadzia : to było do zadnia 5

Pepsi2092: Wzór na sumę miar kątów wewnętrznych dowolnego wielokąta to (n−2)*180⁰ , gdzie n to liczba boków. W zad 1 weź sobie podstaw podziel przez 10 i masz gotowe Więej Ci potem pomogę bo narazie lecem na finał LM pozdro

Pepsi2092: 2. trójkąt jest prostokątny

Pepsi2092: tutaj żadnych obliczeń, to poprostu zależności które trzeba znać

Basiek: 6

	−17+7		3+19
A=(−17, 3 ) B=(7,19)−> środek odcinka M=(		,		)= (−5,10) <− druga ćwiartka
	2		2

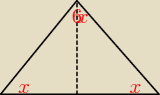
Pepsi2092: 3. x+x+6x=180⁰ bo suma miar kątów w trójkącie tyle wynosi 8x=180||/8 x=10⁰ a kąt między ramionami jest równy 6x ,zatem 6*10=160⁰

Pepsi2092: 4. b) tu też żadnych obliczeń nie ma tylko znajomość teorii, środek okręgu wpisanego w trójkąt to punkt w którym przecinają się dwusieczne, zaś opisanego symetralne

picia: 10

	c
a)R=		=5
	2

	a+b−c		8+6−10
b)r=		=		=4
	2		2

Maadzia: Pepsi2092 a pomożesz mi też ?

picia: w b) oczywiscie 2

Pepsi2092: 7. a−długość boku h−wysokość rombu

	h
sin30=
	a

	1
sin30=
	2

1		h
	=
2		a

a=2h

	a
h=
	2

P=ah

	a2
25=
	2

a²=50 a=√50 a=5√2

Pepsi2092: to dawaj linka szybko, bo jeszcze nie wbiegli na boisko Jak będę umiał to pomogę

Maadzia: hahaha no jasne rozumiem https://matematykaszkolna.pl/forum/147122.html z góry dziekuje

Pepsi2092: 8. Liczysz obwód pierwszego trójkąta. L=16cm teraz okreslasz skalę podobieństwa. W obwodzie i w

	obwód pierwszego
długości boków skala wynosi k=
	obwód drugiego

	16		2
k=		=
	40		5

	2
zatem najdłuższy bok trójkata EFG będzie miał miarę x*		=7cm x=17,5cm
	5

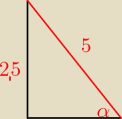
Pepsi2092: 9. to czerwone to drabina Korzystasz z funkcji trygonometrycznych sin

	2,5
sinα=
	5

	1
sinα=
	2

zatem α=30⁰ . Wszystkie wartości poszczególnych funkcjii trygonometrycznych wypadało by znać , a jak nie to są one w karcie wzorów, oczywiście dla kątów od 0−90⁰ nie odczytujesz z tej tabeli przybliżonych wartości tylko masz wczesniej w karcie tabelkę z konkretnymi wartościami sin0=0

	1
sin30=
	2

	√2
sin45=
	2

	√3
sin60=
	2

sin90=1 cos0=1

	√3
cos30=
	2

	√2
cos45=
	2

	1
cos60=
	2

cos90=0 tg0=0

	√3
tg30=
	3

tg45=1 tg60=√3 tg90 − nie istnieje ctg0−nie istnieje ctg30=√3 ctg45=1

	√3
ctg60=
	3

ctg90=0

Karolina!!: ludzie dzieki jesteście mega! ratujecie mi tyłek dzieki**

Karolina!!: Jeszcze mam 5 zadanek pomożecie prosze* 11. Wokręgu o środku O poprowadzono cieciwę AB. Jeden z kątów trójkąta AOB ma miarę 96stopni. Wyznacz miarę kąta zawartego między cięciwą AB a styczną do okręgu poprowadzoną w punkcie A. 12. Oblicz wysokość oraz pole trójkąta równobocznego, na którym opisano okrąg o promieniu 6 cm. 13. Wyznacz równanie okręgu, którego średnicą jest odcinek AB, jeśli A=(1,2) i B=(7,2). Sprawdż, czy punkt C=(2,−3) należy do tego okręgu. Narysuj ten okrąg, 14. Oblicz pole trapezu prostokątnego, którego podstawy maja długość 20 i 8, a kąt ostry tego trapezu jest równy 30 stopni. 15. Znajdz wysokość rombu o boku równym 13 i przekątnej wynoszącej 24. To ostatnie 5 zadanek

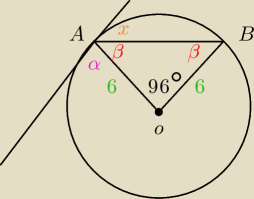
Maadzia: 11. trójkąt jest równoramienny wiec kąty przy podstawie ma takie same zatem: 180−96=84 84:2=42 β=42 α=90 ponieważ styczna jest prostopadła zatem: 180 −(42+90) =48 x=48

Maadzia: kurcze nie wiem jak to zrobilam ale przeczytałam zad 11 razem z 12 i mi wyszlo ze trójkąt jest równoramienny przepraszam to co wysłalam jest zle

Karolina!!: spoko spoko ale itak dalej czekam na pomoc:((

Maadzia: chociaż w sumie jak tak sie tak nad tym zastanawiam to chyba nie jest to zle . Niech to ktos jeszcze sprawdzi xD

Pepsi2092: Dobrze jest , a trójkąt zawsze w takim przypadku jest równoramienny bo ramiona mają długość promienia

Karolina!!: Pepsi2092 prosze pomóż z resztą:((

Maslanek: Napisz co jeszcze jest do zrobienia...

Karolina!!: 12. Oblicz wysokość oraz pole trójkąta równobocznego, na którym opisano okrąg o promieniu 6 cm. 13. Wyznacz równanie okręgu, którego średnicą jest odcinek AB, jeśli A=(1,2) i B=(7,2). Sprawdż, czy punkt C=(2,−3) należy do tego okręgu. Narysuj ten okrąg, 14. Oblicz pole trapezu prostokątnego, którego podstawy maja długość 20 i 8, a kąt ostry tego trapezu jest równy 30 stopni. 15. Znajdz wysokość rombu o boku równym 13 i przekątnej wynoszącej 24.

Karolina!!: zostały te zadania.. do jutra musza byc zrobione:(

Karolina!!: pomocy... ratunkuuuu:(( opresja:((

Sławek.: zaraz zrobimy

Sławek.: 6 = 2/3h , więc h = 9 h = a√3/2 9 = a√3/2 18 = a√3 a = 18/√3 a = 6√3 Pole = a²√3 / 4 P = 108√3 / 4 P = 27√3

Pepsi2092:

	a√3
12. wysokość trójkąta równobocznego wyraża się wzorem h=
	2

	1		1		a√3		a√3
zaś promień okręgu wpisanego w trójkąt stanowi		h=		*		=		,
	3		3		2		6

gdzie a rzecz jasna długość boku trójkąta

	2		2		a√3		a√3
ale promień okręgu opisanego na tym trójkącie stanowi		h=		*		=
	3		3		2		6

Pepsi2092:

	a√3
znaczy się tam masz		, na końcu bo chochlika walnąłem
	3

Sławek.: 2. Wyznaczasz środek tej prostej. S = [(Xa + Xb / 2 ) , (Ya + Yb/2) ] (Xa = 1 , Xb = 7) (Ya = 2, Yb = 2) Liczysz odległość środka S od dowolnego z punktów A lub B. Posłoż się wzorem: np.: |SA| = √(xb − xa)² + (yb−ya)²

Pepsi2092: Te zadania sprawdzają podstawową wiedzę i podstawowe założenia które musisz znać, dlatego popracuj trochę nad tym i poszukaj na własną rękę tutaj na forum opisów do poszczególnych działów , bo jak odwalimy całą robotę to tylko przepiszesz a nic sie nie nauczysz a matura nieubłagalnie się zbliża

Sławek.: ta odległość to Twoje R. A Twoje S to kolejno a i b. Podstawiasz do wzoru: (x−a)² + (y−b)² = r² i masz wzór okręgu

eveluxaa : Dzięki