Dowód - dwusieczne aneta-17: Udowodnij,że dwusieczne kątów wewnętrznych w dowolnym trójkącie przecinają sie w jednym punkcie, który jest środkiem okregu wpisanego w ten trójkąt. Bardzo prosze, pomóżcie

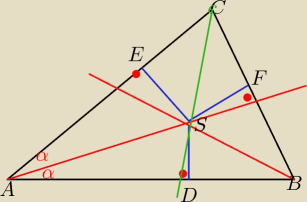
Basia: z definicji dwusiecznej masz : ∡DAS = ∡EAS ponadto ∡ADS = ∡AED (to już nie z definicji, rysuję sobie prostopadłe) czyli również ∡ASE = ∡ASD bok AS wspólny stąd na mocy cechy kbk mamy, że tr.AES i tr.ADS są przystające a stąd wynika, że SD=SE analogicznie udowodnisz, że SF = SD a stąd masz, że SF=SE czyli tr.SEC i tr.SFC są przystające ⇒ ∡ECS = ∡FCS ⇒ pr.CS jest dwusieczną

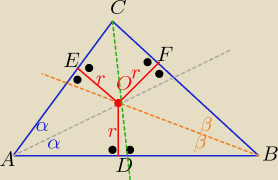
Eta: 2 sposób Z własności dwusiecznej: każdy punkt leżący na dwusiecznej kąta jest równo odległy od ramion tego kąta Zatem skoro punkt O jest punktem przecięcia dwusiecznych AO i BO to: |OD|=OE| i |OD|= |OF| ⇒ |OE|=|OF| czyli punkt O leży też na dwusiecznej kąta ACB Wniosek : punkt przecięcia dwusiecznych kątów trójkąta jest środkiem okręgu wpisanego w ten trójkąt o promieniu długości r c.n.u.

aneta-17: dziekuje bardzo