długości podstaw trapezu Ambryll: oblicz długości podstaw trapezu równoramiennego o polu powierzchni równym 8√2 w którym przekątna jest trzy razy dłuższa od wysokości, a ramię ma długość 4

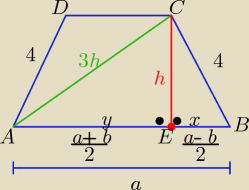
Eta: a, b −−− długości podstaw trapezu

	a−b		a+b
wiadome ,że x=		, y=
	2		2

Z tw. Pitagorasa w ΔAEC

	a+b
y2= 9h2−h2 ⇒ y=		= 2√2*h
	2

	a+b
P=		*h = 2√2*h*h
	2

z treści zadania 2√2h²= 8√2 ⇒ h= 2

	a+b
to		= 2√2*h ⇒ a+b= 8√2
	2

z tw. Pitagorasa w ΔEBC x²= 4²−h² ⇒ x²= 12

	a−b
x=		= 2√3 to: a−b= 4√3
	2

Rozwiąż układ równań: a+b= 8√2 i a−b= 4√3 dokończ...........

hwdtel:

⎧	a=4√3 + 2√2
⎩	b=4√3 − 2√2