mam na jutro 30 zad do rozwiązania. czy mógłby mi ktoś pomóc? Dominika: mam na jutro 30 zad do rozwiązania. czy mógłby mi ktoś pomóc?

Basiek: Tak.

Eta: Troszkę za mało, jak na jutro

Mateusz: Wrzucaj po kolei a się zobaczy

Dominika: podaj mi swój email to wyśle Ci zdjęcia zadań

Eta:

Basiek: A może wrzuć na jakiś serwer i ten... podaj link?

Mateusz: Właśnie jest tyle darmowych serwerów a w końcu podobno mamy społeczeństwo informacyjne

konrad92: i gdzie te zadania?

Basiek: Wszyscy się czają i czekają ♥.

Mila: Do Basiek, ładne zadanie u Marcysi.

Mateusz: No właśnie oczekujemy w napięciu i pełnej gotowości do akcji

konrad92: widać olewa nas heh

Dominika: Oblicz tg12* tg78 + cos (−240)

Dominika: wyznacz długość środkowej w trójkącie prostokątnym o przyprostokątnych o długości 3 cm i 4 cm, poprowadzonej na przeciw prostokątną.

Dominika: 3). określ zbiór wartości funkcji f(x) = −2 (x−1)(x+3)

Basiek: 3. f(x)_min : p=1+(−3)=−2 f(−2)= −2*(−3)*1=6 ZW=(−∞,6>

Dominika: 4. rozwiąż nierówność (x−2)³>(x+2)³

Dominika: 5. oblicz pole koła opisanego nierównością x² + y² − 2x + 4y − 11 ≤ 0

Dominika: 6. wyznacz sumę wszystkich liczb naturalnych dwucyfrowych podzielnych przez 3.

ewa: tg12*tg(90−12)+cos240=tg12ctg12+cos(360−120)=1+cos120=1+cos(180−60)=1−cos60= =1−U{1}{2]=U{1]{2]

ewa:

	1		1
=1−		=
	2		2

Dominika: 7. wielokąt foremny ma 54 przekątne. ile ma boków?

ewa: cos(−240)=cos240 ( wynika to z parzystości funkcji cos)

Mateusz: pole koła to πr² −2a=−2 a=1 −2b=4 b=−2 c=−11 r=√a²+b²−c=... wiec P_kola=...

Basiek:

	n(n−3)
7) przekątne		=54 108=n2−3n n=−9 lub n=12 ale n>0, stąd ma 12 boków.
	2

ewa: ad3 ) Wykresem jest parabola ramionami skierowanymi do dołu i wierzchołku x=−2 y=6. czyli wartośc max wynosi 6 a więc zbiorem wartości jest (−∞,6>

ewa: 6) 12+15+18+...+96+99=? mamy tu ciąg arytmetyczny a₁=12 r=3 n=30 : bo a_n=a₁+(n−1)*r 99=12+(n−1)*3 87=(n−1)*3 n=30 a₃₀=99

	12+99
S30=		*30=111*15=1665
	2

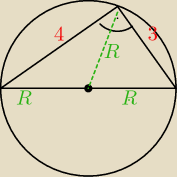
ewa: Środkowa jest równa tutaj promieniowi okregu opisanego na tym trójkącie, a przeciwprostokatna jest średnicą tego okregu. c²=3²+4² c=5 2R=5 R=2,5

Mila: [P[Wyznacz długość środkowej w trójkącie prostokątnym o przyprostokątnych o długości 3 cm i 4 cm, poprowadzonej na przeciw prostokątną]] c²=3²+4² c=5 środkowa poprowadzona z wierzchołka kąta prostego jest równa połowie przeciwprostokątnej. (jest długość promienia okręgu opisanego na tym Δ) s=2,5.

Dominika: http://imageshack.us/photo/my-images/826/skanowanie00031.jpg/ http://imageshack.us/photo/my-images/839/skanowanie0003cm.jpg/

Mila: 4) Rozwiąż nierówność (x−2)³>(x+2)³ x³−3*x²*2+3*x*4−8>x³+3*x²*2+3*x*4+8 x³−6x²+12x−8>x³+6x²+12x+8 −12x²−16>0 f(x)=−12x²−16 przyjmuje tylko wartości ujemne, brak rozwiązania

Basiek: 12 wzory: https://matematykaszkolna.pl/strona/503.html a+b+c=18 => p=9 P=√9(9−5)(9−6)(9−7)= √9*4*3*2= √216=2√54=6√6

	2P		12√6		2√6
r=		=		=
	a+b+c		18		3

Basiek: 25 f(x)= √x²+4x+4= |x+2| To chyba umiesz narysować

Mila: 12) p− połowa obwodu Δ p=(5+6+7):2=9 P_Δ=p*r Obliczam pole z wzoru Herona P_Δ=√9*(9−5)*(9−6)*(9−7)=√9*4*3*2=√36*6=6√6 6√6=9*r

	6√6		2√6
r=		=		−promień okręgu wpisanego w dany okrąg.
	9		3

Basiek: To ja z drugiej kartki, żeby się nie powtarzało. 31 x≠0 i x⁴−6x²=0 ⇔ x²(x²−6)=0⇔ x²(x−√6)(x+√6)=0 ⇔ x=0 (sprz) x=√6 i x=−√6

ewa: 10) Niech p=[x,y] p⊥v ⇒ p◯v=0 ⇒ x*4+y*(−1)=0 ⇒ y=4x u◯p=10 ⇒ −3x+2y=10 ⇒ −3x+8x=10 ⇔5x=10 ⇒ x=2 y=8 p=[2,8]

Basiek: 32 Z tw. Bezout'a: W(−1)=8−17−3−2−24=−38

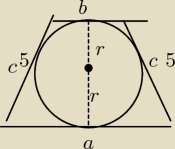
Mila: 16) a+b=2c −sumy długości boków przeciwległych są równe a+b=2*5 a+b=10 h=2r

	a+b
Ptrapezu=		*2r
	2

Basiek: 29 Wyznaczę prostą AB:

	1+2		3
aAB=		=
	−3+7		4

	3
y=		x+b
	4

1=−4+b => b= 5

	3
y=		x+5
	4

Sprawdzam. czy pkt C należy do prostej

	3
y=5*		+5 ≠ 7
	4

Nie są współliniowe (chyba, że gdzies w obliczeniach się machnęłam)

Basiek: 30 m≠1 prostopadłe, gdy a pierwszej prostej −2

	1		1
−2=		⇔ −2m+2=1 => m=
	m−1		2

123: Zad. 24 x₁x₂ = 3

c
	= 3
1

c = 3 (x₁ − x₂)² = 4 x₁² + x₂² − 2x₁x₂ = 4 (x₁ + x₂)² − 2x₁x₂ − 2x₁x₂ = 4 (x₁ + x₂)² − 4x₁x₂ = 4

	−b		c
(		)2 − 4		= 4
	1		1

b² − 4c = 4 b² − 4*3 = 4 b² − 12 = 4 b² = 16 ⇒ b² = 16 > 4c = 12 b = 4 v b = −4 Więc: c = 3 i b = 4 lub c = 3 i b = −4

Basiek: 29 ={0,1,2,3,4} O ile zakładamy, że 0 jest naturalną.

ewa: 15) |x+3|+|x−1|=5 a) x<−3 b) −3≤x<1 c) x≥1 −x−3−x+1=5 x+3−x+1=5 x+3+x−1=5 x=−3,5 4=5 sprzeczne x=1,5 odp. x=−3,5 lub x=1,5

123: Zad. 27 x ∊ (−∞, 5) ∩ N ⇒ x ∊ {0, 1, 2, 3, 4}

Basiek: 26 S_n−S_n−1=a_n 2n²−3n−2(n−1)²+3(n−1)= 2n²−3n−2(n²−2n+1)+3n−3= 2n²−3n−2n²+4n−2+3n−3= 4n−5

Mila: 7) m,4m−2,9m tworzą ciąg geometryczny warunek: (4m−2)²=m*9m rozwiąż ten warunek 14) warunek: a≠0

	1		9
a−		≤		⇔
	a		20

a2−1		9
	≤		⇔
a		20

a2−1		9
	−		≤0 dokończ
a		20

Basiek: 22 a+b=5=> a=5−b ab=7=> b(5−b)=7 => b²−5b+7=0 i Δ<0 cnu

ewa: 13)

4m−2		9m		1
	=		m≠0 i m≠
m		4m−2		2

7m²−16m+4=0 √Δ=12

	16−12		2		16+12
m1=		=		lub m2=		=2
	14		7		14

Basiek: 19 W(1)=(1−2)^2m−1= 1−1=0

Basiek: 18 y=kx²+1 y=x Podstawiam drugie do pierwszego x=kx²+1 => kx²−x+1=0 Rozważmy 1^o k=0 y=1 i y=x (przetną się), więc k≠0

	1
2o k≠0 Δ<0 Δ=1−4k< 0 dla k<		i k≠0
	4

123: Zad. 21 Dla x ∊ <0, +∞)

x		x − x
	+ cos		= 0
x		2

1 + cos 0 = 0 1 + 1 = 0 2 ≠ 0 / sprzeczność − brak rozwiązań Dla x ∊ (−∞, 0)

x		x + x
	+ cos		= 0
−x		2

−1 + cos x = 0 cos x = 1

	π		π
x ∊ ( −		+ kπ, −		>, gdzie k < 0 i k ∊ C−
	2		2

Basiek: Ja dalej nie robię, bo mi się ....nie chce. Dominika− Tobie radzę zacząć robić zadania, bo koniec drugiej klasy, to najwyższa pora, by zacząć uczyć się do matury. Poza tym, jeśli nauczyciel chce Was przygotować, daje Wam kserówki z zadaniami.... to na Twoim miejscu bym się cieszyła i sobie je robiła.

123: Oj tam jest cos x = 1, więc x ∊ (−2π + 2kπ, −2π> gdzie k < 0 i k ∊ C⁻

Dominika: dzięki Bastek za pomoc

Dominika: Basiek*

picia: a inni odwalili kawal roboty z tego co widze..

Dominika: wszystkim bardzo dziękuje

Dominika: zostały jeszcze zad 1, 7, 17, 20, 23 i 28. może ktoś umie je rozwiązac

Dominika: zostały jeszcze zad 1, 7, 17, 20, 23 i 28. może ktoś umie je rozwiązac

asdf: 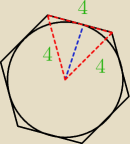Zad. 28 Sześciokąt foremny o boku 4 cm jest opisany na okręgu. Oblicz długość okręgu. Długość = obwód

	a√3		4√3
r =		=		= 2√3
	2		2

Ob. = 2πr = 4√3π

Basiek: To ja mogę jeszcze 1 i 7

Dominika: byłabym bardzo wdzięczna

picia: jestescie niemozliwi

Basiek: 1 √|x|−3 więc |x|−3≥0 |x|≥3 ⇔ x≥3 lub x≤−3 => x∊(−∞,−3>∪<3,+∞) x³+4x+5≠0 W(−1)=0 Hornerem: (x+1)(x²−x+5)≠0 x²−x+5≠0, bo Δ<0 => x≠−1 D=(−∞,−3>∪<3,+∞)

Basiek:

25n+1
	<15 i n∊N+
n+5

25n+1<15n+75 10n<74 n<7,4 więc n∊{1,2,3,4,5,6,7} 7 takich wyrazów.

Basiek: To była 7

Dominika: WIELKIE DZIĘKI dobranoc

asdf: Zad. 23 Dane jest równanie z parametrem a: ax − a² = √3x − 2a√3 + 3 DO SPRAWDZENIA DO SPRAWDZENIA DO SPRAWDZENIA ax − a² = √3x − 2a√3 + 3 ax − a² − √3x + 2a√3 − 3 = 0 −a² − 2a√3 + ax − 3 − √3x = 0 −a² − (2√3 − x)a − 3 − √3x = 0 PARAMETRY: A = −1 B = −(2√3 − x) = x − 2√3 C = − (3 + √3x) = −√3x − 3 Δ = 0 << jedno rozwiązanie Δ = (x − 2√3)² − 4 *(−1)* (−1)(3 +√3) x² − 4x√3 + 12 − 12 − 4√3 = 0 x² − 4x√3 − 4√3 = 0 PARAMETRY: A = 1 B = −4√3 C = −4√3 Δ = 0 << jedno rozwiązanie i dalej dla x itd...dobrym tropem idę?

Basiek: Hm, ja bym to zrobiła tak: x(a−√3)=a²−2a√3+3 x=U{a²−2a√3+3}{a−√3) i a≠√3 1 rozw. dla Δ=0 Δ=12−12=0 a∊R/{√3} Chyba...

asdf: x₀ = √3 ∉ D, więc a∊R/√3 czy a ∊ R?

Basiek: 20 , bo proste z tw. cos dla ΔABD 49=x²+y²−xy x+y=13 (z odwodu) /² => x²+y²+2xy= 169 Odejmujemy stronami: 3xy=120 −> xy=40 i x+y=13 => x=13−y y(13−y)=40 i y>0 => y=5 i x=8

Basiek: a∊R/ {√3} Przecież napisałam

Basiek: A to 17.... albo to jest takie proste, albo dalej tego nie umiem

	π		π
sin(x−		)∊<−1,1> => 2sin(x−		)∊<−2,2>
	3		3

	π
zaś całe y=2sin(x−		)+1 ∊ <−1,3>
	3

Basiek: Mam nadzieję, że nigdzie nie ma takich błędów, za które (znów będę musiała się wstydzić. Ale u mnie wszystkie obliczenia raczej powinny być sprawdzane. Dobranoc