Na okręgu o promieniu 3 opisano trójkat równoramienny o kącie przy wierzchołku r Marcysia: Na okręgu o promieniu 3 opisano trójkat równoramienny o kącie przy wierzchołku równym 120 stopni. Oblicz długość boków tego trójkata.

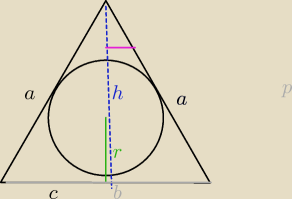
konrad92: r=¹₃h h=9 sin60⁰=^c₁₈ c=9√3 sin30⁰=⁹_a a=18 b=2*c=18√3

konrad92: może być?

Mila: konrad, nie .Pierwsza linijka −błąd.

Basiek: Ja hm....

	1		1
P=		a2sin120=		a2
	2		4

	(2b+a)r		(2b+a)3
P=		=
	2		2

	1
P=		bh
	2

+ Pitagoras Powinno wyjść

Basiek: No nie, tam nawet mamy trójkąt charakterystyczny.

	1
h=		a
	2

konrad92: sorki pomagam siostrze i zmiksowałem sorki dobra napiszcie całość jak zrobić bo nie ogarniam jakoś

konrad92: to tak jak zrobiłem nie można?

Basiek:

	1
r=		h jest tylko w równobocznym, a ten jest równoramienny
	3

Basiek: A masz odp?

konrad92: ja czy marcysia?

Basiek: Marcysia, chcę wiedzieć, jaka jest poprawna odp. Bo planimetria to moja pięta Achillesa

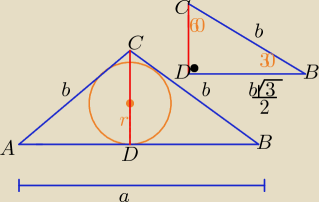
Eta: a=2*|DB|=b√3

	2P		1		1		√3
r=		P=		*b*b*sin120o=		b2*
	a+b+b		2		2		2

	b2√3
to 2P=
	2

	b2√3   2
3=
	a+2b

......

	b2√3
3(b√3+2b)=		/:b≠0
	2

√3b= 12+6√3 ⇒ b= 4√3+6 to a= b√3= 6√3+12

Basiek: Wyszło mi, kto by pomyślał, ze takie rzeczy się zdarzają.

Eta:

konrad92: no ok to mamy h=¹₂a i co z tym dalej zrobić bo teraz nie wiem?

Basiek: A Eta jak zawsze taaaakie ładne.

konrad92: aaa wyższy poziom