całki iterowane Kwachu: Mam problem w zadaniu, gdzie mam ∫∫_D(2x+3y+1)dxdy na ograniczonym obszarze trójkąta D w pkt: (1,3) (−1,−1) (2,−4) W ogóle nie mam pojęcia jak za to się zabrać, bo nie wiem jak zapisać całki iterowane. Na początku myślałem, żeby znaleźć proste dla każdego z tych pkt., ale to chyba jednak nie tą drogą się robi. Dzisiaj mam egzamin z matmy i wiem, że dokładnie takie zadanie może się pojawić, a jest to z materiału, który nie jest już przerabiany na zajęciach (za mało czasu na przerobienie wszystkich list, a wymagają to na egzaminie, więc trzeba uczyć się samemu ) Bardzo był bym wdzięczny, jak by ktoś mi to rozpisał do momentu jak trzeba będzie obliczyć całkę nieoznaczoną. chodzi mi o to, żeby ktoś mi pomógł zapisać całkę iterowaną

Trivial: Tak, trzeba znaleźć proste, a potem jakoś ustalić granice całkowania. Bez rysunku się nie obejdzie.

Kwachu: pomożesz mi zapisać te całki? proste to: y=2x+1 y=−7x+10 y=−x−2

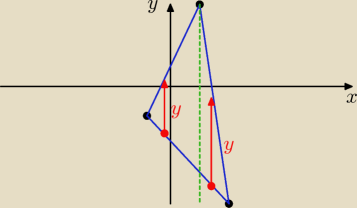
Trivial: Wyznaczasz wszystkie równania prostych, rozbijasz całkę na całkę po trójkącie na lewo od zielonej linii i na prawo od zielonej linii.

Kwachu: więc to będzie ₋₁∫ ¹ dx∫ (nie wiem z czego całka) +₁∫² dx ∫też nie wiem jaka czy to ma byc coś takiego? niestety nie wiem jak to zapisać

Trivial: Całka z tego samego co było, tj. (2x+3y+1)

Kwachu: ale oznaczona w jakim przedziale

Trivial: granice po x masz dobrze dobrane. Granice po y dobieramy patrząc jak 'idziemy', czyli od jakiej prostej do jakiej prostej. Na lewo od zielonej linii idziemy od y=−x−2 do y=2x+1. Na prawo od zielonej linii idziemy od y=−x−2 do y=−7x+10.

Kwachu: więc ₋₁∫¹ dx _y=−x−2∫^y=2x+1 (2x+3y+1)dy+ ₁∫² dx _y=−x−2∫^y=−7x=10 (2x+3y+1)dy ?

Trivial: tak

Kwachu: dzięki wielkie kolejne pytanie, zawsze jam mamy taki trójkąt jako obszar, to dzielić go na 2 mniejsze idąc od wierzchołka tego trójkąta?

Trivial: To zależy od przypadku. Trzeba narysować i zobaczyć jak to podzielić. Nie ma jednej złotej rady.