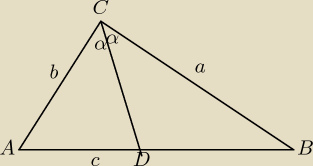Wykaż, że jeśli lABl=c, lBCl=a, lACl=b, a CD jest odcinkiem dwusiecznej kąta ACB, zawartej w
| bc | ac | |||
trójkącie, to lADl= | , a lBDl= | |||
| a+b | a+b |
| b | a | ||
= | |||
| x | c−x |
| bc | ||
ax+bx= bc ⇒ x=|AD|= | ||
| a+b |
| bc | ac+bc−bc | ac | ||||
i c−x= |BD|=c− | = | = | ||||
| a+b | a+b | a+b |
| |AD| | |DB| | |AD| | c−|AD| | ||||
= | i (*)|DB|=c−|AD| ⇒ | = | ⇔ | ||||
| b | a | b | a |
| bc | ||
⇔ |AD|a+|AD|b=bc ⇔ |AD|(a+b)=bc ⇒ |AD|= | , więc stąd i z (*) | |
| a+b |
| bc | ac+bc−bc | ac | ||||
|DB|=c− | ⇔ |DB|= | = | . ...  | |||
| a+b | a+b | a+b |