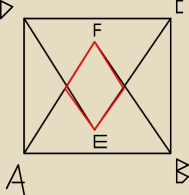
HELPP!!!! JUSTYNKA: POMOCY: Bok kwadratu ABCD ma długość równą 2. Oblicz pole czworokąta będącego częścią

	8√3
wspólną trójkątów równobocznych ABF i DEC. wynik powinien być		− 4 i w
	3

rzaden sposób nie może mi taki wyjść..

Mickej : zaznacz na rysunku u siebie w zeszycie prostą łączącą środki przeciwległych boków najlepiej srodek boku |AD| ze środkiem |BC| może to ci coś objaśni

JUSTYNKA: zrobiłam już tak ale mi zupełnie inne wyniki wychodzą

tim: Ja też próbuję!

JUSTYNKA: to jak komuś się uda to prosze napiszcie bo to ważne..

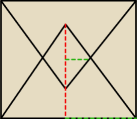
Mickej : skorzystaj z trójkątów podobnych to na pewno ci się uda ta czerwona przerywana linia to h=√3

JUSTYNKA: czyli chodzi tu o twierdzenie Talesa?

Mickej : tak

JUSTYNKA: dzięki bardzo

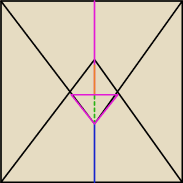
tim: Mickej.. pewnie masz łatwiejszy sposób, ale ja proóbuję takim. Ciężkie zonaczenia ale są Wysokość trójkąta równobocznego = a√3 / 2 = √3 Odcinek zielony = √3 − 1 Nasza figura ma szerokość = 2(√3 − 1) No ok Trójkąt różowy jest równobonczy, a zielona linia (√3 − 1) jest jego wysokością. a√3 / 2 = √3 − 1 Wyznaczamy a = 6 − 2√3 / 3 = 2 − (2√3 / 3)

	(2√3   (2 − ) * 2(√3 − 2)   3
Pole = d1 * d2 / 2 =		=
	2

	2√3		8√3
2√3 − 2 − 2 +		=		− 4
	3		3

tim: O boże ja trochę inaczej

JUSTYNKA: dzięki

tim: Żem się namęczył...

JUSTYNKA: no ja też i to przez cały dzień