rekurencja
ksiądz: Zadanie za pomocą równania rekurencyjnego:
Niech (an) , n∊N oznacza liczbę sposobów pokrycia prostokąta (2 x n) , n∊N , kostkami domino
o wymiarach(2 x 1). Rozważyć przypadki szczególne n=2,3,4 i uzasadnić wzór rekurencyjny.
Przyjąć a0=1.
Pomoże ktoś ?
17 maj 00:12
ksiądz: hej
17 maj 00:23
ksiądz: pomoże ktoś jeszcze
17 maj 01:41
Artur z miasta Neptuna:
hmmm
no to lecimy:
n=1
to na 1 sposób
n=2
to na 2 sposoby (w pionie dwa układasz, albo w poziomie dwa układasz)
n=3
to na 3 sposoby (w pionie, w poziomie 2+1 w pionie −−− na dwa sposoby)
n=4
to na 5 sposobów (w pionie, dwa w pionie i dwa w poziomie −−− na 3 sposoby, cztery w poziomie)
n=5
to na 8 sposobów (w pionie, trzy w pionie i dwa w poziomie −−− na 4 sposoby, jeden w pionie i
cztery w poziomie −− na 3 sposoby)
n = 6
to na 13 sposobów (w pionie, cztery w pionie i dwa w poziomie −−− na 5 sposobów, dwa w pionie i
cztery w poziomie −−− na 6 sposobów, sześć w poziomie)
itd.
i teraz kombinuj wzór rekurencyjny
17 maj 09:19
Artur z miasta Neptuna:
n=7
to na 20 sposobów (w pionie, pięć w pionie i dwa w poziomie −−− na 6 sposobów, trzy w pionie i
cztery w poziomie −−− na 9 sposobów, jeden w pionie i sześć w poziomie −−− na 4 sposoby)
już widzisz jakiś związek rekurencyjny
;>
17 maj 09:22
Artur z miasta Neptuna:
sorki
dla n=7
jest 21 sposobów oczywiście
17 maj 09:23
ksiądz: ale to chyba chodzi o wszystkie kombinacje czyli dla n=3 trzeba chyba wszystkie kombinacje
rozpisać tych kostek domino. czyli np: przyjmnijmy że 1−pierwsza kostka 2−druga 3 trzecia
kostka
to w tedy możemy np : 123 132 213 231 ...itd czyli 3! = 6
dla 4 bedzie już 4!=24
czy nie tak czasem będzie
?
17 maj 13:59
ksiądz: a zresztą Arturze jeżeli przyjąć twoją wersję to przecież wymiari prostokąta są 2xn a domina
2x1 w takim razie kostki mieszczą można układać tylko w pionie a nie w poziomie czyli dla
n=5 − 5 sposobów dla n=7 − 7 sposobów
17 maj 14:13
Artur z miasta Neptuna:
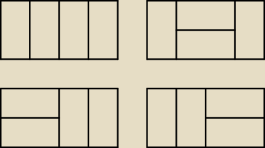
podałem jak wyglądają sposoby rozłożenia dla n=4 (czyli prostokąt 2x4)
17 maj 14:18
Artur z miasta Neptuna:
a w zadaniu masz do czynienia z liczbami Fibonacciego, czyli sztandarowym równaniem
rekurencyjnym stopnia 2.
F0 = 1
F1 = 1
Fn = Fn−1 + Fn−2
17 maj 14:21
Artur z miasta Neptuna:
W treści zadania nie ma napisane, że kostki są rozróżnialne ... czyli NIE SĄ one rozróżnialne
Nawet dla rozróżnialnych, to mój wynik trzeba uwzględnić * ilość kombinacji elementów domina
17 maj 15:05
ksiądz: aha już rozumiem
to wynik będzie :
| 1 | | 1+√5 | | 1−√5 | |
| *[( |
| )n+1( |
| )n+1] |
| √5 | | 2 | | 2 | |
taki
17 maj 15:28
ksiądz: jak mógłbyś mi sprawdzić był bym bardzo wdzięczny
17 maj 15:43
Artur z miasta Neptuna:
a co to jest
skąd te pierwiastki
17 maj 16:08
ksiądz: no obliczam
F
n=F
n−1+F
n−2
sposobem Równania rekurencyjnego rzędu drugiego liniowego o stałych współczynnikach
czyli
x
n=px
n−1 + qx
n−2 n≥2
dane jest wzorem:
| | an−bn | | an−1−bn−1 | |
xn= |
| x1 − ab |
| *x0 |
| | a−b | | a−b | |
gdzie a i b to pierwiastki równania kwadratowego s
2=ps+q
17 maj 17:36
Krzysiek: 'dane jest wzorem'
I Ty znasz ten wzór na pamięć?
zacząłem rozpisywać ale coś mi nie chce wyjść Twoja postać (co wyżej napisałeś)
mając: równanie rekurencyjne: np.: Fn=Fn−1+Fn−2
to równanie charakterystyczne to: x
2 =x+1 (czyli to co wyżej napisałeś: s
2 =ps+q)
| | 1−√5 | |
i pierwiastki tego równania to: x1 = |
| |
| | 2 | |
zatem F
n jest postaci:
F
n =c
1 ( x
1 )
n +c
2 (x
2 )
n
i teraz wstawiając warunki początkowe: F
0 =1 i F
1 =1 wyliczasz c
1 i c
2
17 maj 17:55
ksiądz: no tak mi wychodzi rozpisując te wzory
a czy jest gdzieś o tym napisane że x
2 =x+1 jest równaniem charakterystycznym do
F
n=F
n−1+F
n−2 bo skąd miałbym niby to wiedzieć
17 maj 18:05
Krzysiek: tzn: szukasz rozwiązania w postaci: Fn =xn (analogia do równań różniczkowych)
wstawiasz do równania: Fn =Fn−1 +Fn−2
Fn −Fn−1 −Fn−2
xn −xn−1 −xn−2 =0
dzielisz obustronnie przez: xn−2 (możesz bo to funkcja wykładnicza ≥0 )
i otrzymujesz: x2 −x−1=0
17 maj 18:09