Proszę o sprawdzenie badania przebiegu Kan: Witam. Bardzo prosze o sprawdzenie bo nie mogę dojśc gdzie popełniam błędy. http://img220.imageshack.us/img220/295/15759958.jpg http://img259.imageshack.us/img259/1414/65027985.jpg http://img707.imageshack.us/img707/305/47875461.jpg http://img854.imageshack.us/img854/8303/46616437.jpg Na końcu tabela z błędami.

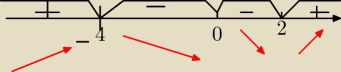
Aga1.: f^'(x)>0⇔x∊(−∞,−4)U(2,∞)

Aga1.: Źle, bo 0 nie jest pierwiastkiem parzystej krotności.

Aga1.: Poprawione : 2 jest pierwiastkiem dwukrotnym teraz już (zdaje się),że wszystko będzie dobrze

Kan: hm... ale dlaczego przechodzisz przez 0?

Aga1.:

(x−2)2(x+4)
	>0⇔
x3

(x−2)²(x+4)x³>0 i x≠0 x=2 −−−−pierwiastek dwukrotny x=−4−−pierwiastek jednokrotny x=0−−pierwiastek trzykrotny.( przy 0 kółeczko puste) f^'(x)>0⇔x∊(−∞,−4)U(0,2)U(2,∞)

Kan: wg tego co napisałaś wykres końcowy i tabela będą się zgadzać, ale mam jedną wątpliwość. Dlaczego na wykresie uwzględniasz mianownik funkcji, skoro całą nierówność mnoży się przez x³ żeby się pozbyć mianoiwnika i dopiero wtedy wyciąga miejsca zerowe.

Aga1.: Równanie mnożysz przez mianownik, a nierówność przez mianownik do kwadratu.

Kan: ahaaa..., Aga1 jestem Ci niezmiernie wdzięczny za pojaśnienie. Pozdrawiam.

Kan: Jaby ktoś miał chwilkę to prosiłbym o sprawdzenie asymtoty ukośnej bo przecina mi się z poprawną już funkcją

Artur z miasta Neptuna: wykres funkcji: http://www.wolframalpha.com/input/?i=plot+%28x-2%29%5E2%2F%28x%5E2%29+x%3D-50...50 asymptota ukośna (i pozioma jako szczególny jej przypadek) MOGĄ przecinać wykres funkcji f(x) w jakimś przedziale (a to ma miejsce u Ciebie) ... ale nie w +/− ∞ ... czyli jest wszystko dobrze.

Artur z miasta Neptuna: asymptota ukośna pokazuje tylko gdzie 'ucieka' y dla x = ⁺/₋ ∞

Kan: aha, jeżeli tak to mam już dobrze. Dziękuję za szybką odpowiedź.