Objętość ostrosłupa BigMax: W ostrosłupie trójkątnym wszystkie krawędzie boczne i dwie krawędzie podstawy mają długość b, a kąt miedzy równymi bokami podstawy ma miarę α. Oblicz objętość tego ostrosłupa. Dla jakich α zadanie to ma rozwiązanie? Nie mogę poradzić sobie z tym zadaniem. Najpierw staram się R obliczyć podstawy przy pomocy tw. cos i tw. sin. Wychodzi mi to i potem Pitagorasem staram się obliczyć H. Mimo to wychodzi mi zupełnie inny wynik. Proszę o pomoc. Z góry dziękuje

Mariusz: wydaje mi sie że dla α=60 stopni, bo jeżeli krawędzie boczne sa równe ( wszystkie) to musi to być trójkąt równoboczny w podstawie, moge sie myliś ale ja bym tak to zrobił

@Basia: Nie musi Mariuszu. Jeżeli wszystkie krawędzie boczne są równe to spodek wysokości H jest środkiem okregu opisanego na podstawie. dane: b,α

	a
R =
	2sinα

	a2
sinα2 =
	b

	a
sinα2 =
	2b

a = 2b*sin^α₂ −−−−−−−−−−−−−−−−−−−−−−−−−−

	2b*sinα2
R =
	2sinα

	2b*sinα2
R =
	4sinα2*cosα2

	b
R =
	2cosα2

R² + H² = b²

b2
	+ H2 = b2
4cos2α2

	4b2*cos2α2 − b2
H2 =
	4cos2α2

	b2
H2 =		*(4cos2α2 − 1)
	4cos2α2

	b
H =		*(4cos2α2−1)
	2cosα2

	b*b*sinα
Pp =
	2

	b2*sinα		b
V =		*		*(4cos2α2−1)
	2		2cosα2

	b3*2sinα2cosα2
V =		*(4cos2α2−1)
	2cosα2

V = b³*sin^α₂*(4cos^2α₂−1) jeśli wynik jest inny podaj go może inaczej są przekształcane f.tryg.

@Basia: α∈(0;180) innych ograniczeń nie widzę

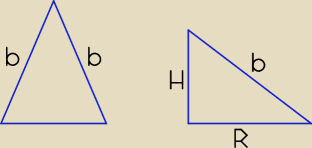
Bogdan: Wskazówki α − miara kąta między ramionami b

	1
Pole podstawy ostrosłupa PP =		b2sinα
	2

R − długość promienia okręgu opisanego na podstawie

	b		b
Z twierdzenia sinusów		= 2R => R =
	α   sin(90o − )   2		α   2cos   2

H − wysokość ostrosłupa Z tw. Pitagorasa H² = b² − R²

Brochu: Do rozwiązania Basi: w tym momencie:

	b2		α
H2=		*(4cos2		−1) pierwiastkując nie spierwiastkowałaś liczby
	α   4cos2   2		2

	α
4cos2		−1, zatem powinno to wyglądać po spierwiastkowaniu:
	2

	b
H=		*√(4cos2α2−1)
	α   2cos   2

ale musimy pamiętać też o tym, że pierwiastkować możemy tylko liczby dodatnie, zatem należy sprawdzić dla jakiego α zachodzi nierówność: 4cos^2α₂−1≥0 do tego dochodzi fakt, ze α∊(0,π) rozwiązujemy i dostajemy α