Zadanie Karola: Dwusieczna kąta prostego w trójkącie prostokątnym dzieli przeciw prostokątną w stosunku 1:3 Oblicz miarę kątów tego trójkąta.

Maslanek: α=45 Po narysowaniu wysokości powstają dwa trójkąty przystające

	h		h
sinα=		, sinδ=		⇒
	b		3x

b sinα = 3x sinδ

	h
sinβ=		⇒ x sinβ = b sinα
	x

x sinβ=3x sinδ sinβ = 3sinδ sin (π/2 − δ) = 3sinδ cosδ = 3sinδ |:sinδ≠0 ctgδ=3... Chyba coś poszło nie tak W każdym razie jest już blisko

Maslanek: Wychodzi jakiś marny kąt 18,435 z tego −,−... Ale coś będzie xD

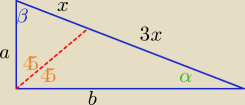
Eta: x>0 Z twierdzenia o dwusiecznej:

3x		x
	=		⇒ b= 3a
b		a

	a		1
tgα=		=		=0,3333 ⇒ α≈ 18,4o
	3a		3

β= 90^o−α=..........

Maslanek: Czyli jednak nie jestem taki głupi . Ale takiego twierdzenia nie znałem Przyda się

Eta:

Maslanek: Tak w ogóle to czy ja właśnie nie udowodniłem go?

Eta: