Funkcja wymierna Adrianek: Witam mam zadane 5 zadań z funkcji wymiernej, 2 zrobiłem z 3 mam niestety problem. oto ich treść:

	3a − x
1. Funkcja f(x)=		jest funkcją homograficzną, której miejscem
	x − 12 b

zerowym jest liczba 6. Funkcja F jest malejąca w każdym z przedziałów: (−∞;4) oraz (4;+∞) wyznacz wartośći parametrów a i b. Napisz wzór funkcji F, naszkicuj jej wykres. Rozwiąż algebraicznie nierównośc f(x)≤1.

	−4x − 5
2 Dana jest funkcja o wzorze f(x)=		. określ dziedzinę funkcji. oblicz
	x + 2

miejsce zerowe funkcji oraz współrzędne punktu w którym wykres przecina oś OY. Podaj

	3
współrzędne wektora o jaki nalezy przesunąć wykres funkcji y=		aby otrzymać wykres
	x

funkcji f. oblicz dla jakiego argumentu wartośc funkcji wynosi 5 3 to chyba najgorsze. wykonaj wskazane działania. podaj konieczne założenia. wynik przedstaw w

	2x4 − 16x		x2 − 4x +4
postaci ułamka nieskracalnego. (		:		−3)*
	x2 + 2x + 4		3

2+5x−3x² / x²+2x (mały problem z zapisem ułamka) z góry dziękuję za wskazówki/ rozwiązania

Mila: 3)zał. x² + 2x + 4 ≠0⇔dla x∊R bo Δ<0 x² − 4x +4≠0⇔(x−2)²≠0 ⇔x≠2 ⋀ x²+2x ≠0⇔x(x+2)≠0⇔x≠0⋀x≠−2

	2x4−16x		x2+2x+4		2+5x−3x2
(		:		−3)*
	x2+2x+4		3		x2+2x

czy tak wygląda ten przykład?

Adrianek: dokładnie tak

Adrianek: jednak jest błąd x²−4x+4 zamiast x²+2x+4

Alois~:

	3a − x
1. masz y=
	x−12b

teraz masz podany ze dla x=6 ( podstawiasz wyzej) y=0 ( tez postaw) x−¹₂b ≠ 0

Mila:

	2x(x3−8)		3		−3(x−2)
(		*		−3)*		=
	x2+2x+4		x2−4x+4		x−1/3

	2x(x−2)(x2+2x+4)		3		−3(x−2)
(		*		−3)*		dokończ
	x2+2x+4		(x−2)2		x−1/3

Mila: Błąd ten zauważyłam.Kopiowałam i dlatego.

Alois~: dalej masz że 6− ¹₂b≠0 z tego wychodzi że b≠−12

Adrianek: w 2 zadaniu wyszły mi takie rozwiązania Df=R\ {−2} miejsce zerowe =4x=5 czyli x=−5/4 współrzędne punktu (0,−5) dla argumentu x=−15/9 a z tym przesunięciem wykresu nie mam pomysłu

Mila: Napiszę jak wykonać wykres

Eta:

	−4x−5
2/ f(x)=		D= R\{−2}
	x+2

	−4x−8+3		−4(x+2) +3		3
f(x)=		=		= −4+
	x+2		x+2		x+2

→ u= [3,−4]

Mila:

	−4x − 5
f(x)=		przekształcam do postaci kanonicznej
	x+2

	−4*(x+2)+8 − 5		−4*(x+2)+3
f(x)=		=		=
	x+2		x+2

	−4*(x+2)		3		3
=		+		=−4+
	x+2		x+2		x+2

	3
f(x)=		−4
	x+2

	3
1) rysujesz wykres funkcji g(x)=
	x

	3
2) przesuwasz równolegle o wektor[−2,−4] otrzymujesz wykres f(x)=		−4
	x+2

Eta: Sorry widzę chochlika oczywiście ma być: → u= [−2,−4]

Adrianek: w zadaniu 1 x=6 czy 3a=6? dalej w tym zadaniu problem dziękuję za takie zainteresowanie i pomoc

Mila: Adrianek, co ustaliłeś w pierwszym?

Mila: Asymptota pionowa x=4 to 1/2b=4⇔b=8 3a=6 a=2

	6−x
f(x)=		przekształć do postaci kanonicznej , tak, jak Ci pokazałyśmy w II zadaniu.
	x−4

?

Adrianek: próbuję coś zrobić z tym miejscem zerowym zrobić i to jest tak jak mówi Alois że za x trzeba podstawic 6 ?

Mila:

3a−6
	=0
6−4

Adrianek: no tak teraz to ładnie widac Rozwiąż algebraicznie nierównośc f(x)≤1. tutaj podstawić za x np 1? to nie wyjdzie bezsens trochę?

Mila:

6−x
	≤1
x−4

6−x
	−1≤0
x−4

6−x		x−4
	−		≤0 dokończ.
x−4		x−4

Adrianek: 6−x−x+4/x−4 = 10−2x/x−4 //(x−4) => −2x⁺18x−40 Δ=4 √Δ=2 x1=4 x2=5 coś tym śladem?

Aga1.: (−2x+10)(x−4)≤0 Krócej: każdy nawias przyrównać do zera −2x+10=0 lub x−4=0 x=5 v x=4 teraz narysuj parabolę ramionami do dołu i odczytaj rozwiązanie uwzględniając dziedzinę.

Adrianek:

	1
x−		b ⇔ x−4 ⇒ x≠4
	2

pomógłby ktoś z wykresem?

ania: u mnie są kwadraciki więc nie wiem co to za równanko

Adrianek: z zadania 1 wyszło y=(6−x) / (x−4) i trzeba do tego szkic wykresu

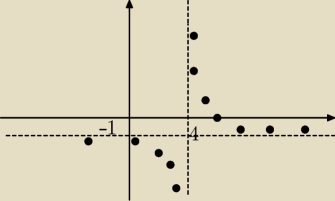
ania: połącz kropki hiprebolą bo mi nie wychodzi

Adrianek: dzięki śliczne. czyli rozwiazanie jak będzie wyglądało?

ania: https://matematykaszkolna.pl/strona/157.gif

Adrianek: z 3 rozumiem te założenia i początek a reszta to czarna magia mógłby ktoś rozpisać to zadanie w całości od początku do końca? obiecuję że sie nauczę

Mila: Adrianek, masz 3 rozpisane; wyjaśniam: x³−8 =(x−2)(x²+2x+4) ze wzoru skróconego mnożenia a³−b³ masz tylko uprościć.