funkcja kwadratowa biedronka: Wyznacz wzór funkcji kwadratowej f, która: b) ma dokładnie jedno miejsce zerowe równe 2, a jej wartość największa w przedziale <4,7> wynosi −2 proszę o pomoc

Beti: f(x) = a(x−2)² −−> bo m.zer. jest 2 wartość największa mieści się w przedziale <4,7>, a m. zer. jest w 2−ce(i tu jest też wierzchołek paraboli), więc wartość największa nie jest w wierzchołku paraboli, tylko na jednym z końców podanego przedziału. Skoro W_najw. jest liczbą ujemną, to ramiona paraboli muszą być skierowane na dół, a to oznacza, że W_najw. = f(4) = −2.

	1
Zatem: f(4) = a(4−2)2 = 4a i 4a = −2 −−> a = −
	2

	1		1
Wzór tej funkcji, to: f(x) = −		(x−2)2 = −		x2 + 2x − 2
	2		2

Mam nadzieję, że zrozumiałaś Jakby co, to dopytaj.

biedronka: a pomozesz mi jeeszcze z tym c) ma jedno z miejsc zerowych równe 3, maksymalny przedział, w którym jest ona malejąca, to <1, nieskończoność) a jej wartość największa w przedziale <−7,−6> wynosi −45 błagam o pomoc

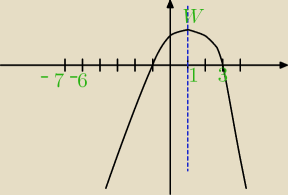
Beti: Podobna sytuacja: 2 miejsca zerowe: f(x) = a(x−3)(x−x₂) Skoro funkcja maleje w przedz. <1,oo), to znaczy, że wierzchołek tej paraboli jest w punkcie W = (1,q), ramiona ma skierowane w dół oraz, że parabola jest symetryczna względem prostej x=1. Oznacza to, że drugie m. zer. tej funkcji jest w (−1) −−−> PATRZ RYSUNEK. Funkcja ma więc wzór: f(x) = a(x−3)(x+1). Ramię paraboli w przedziale <−7,−6> rośnie, więc warość większą osiąga dla x = −6, a zatem: f(−6) = a(−9)(−5) = 45a i 45a = −45 −−−> a = −1 Ostatecznie: f(x) = −(x−3)(x+1) = −x²+2x + 3