oblicz długość łuku głupol: oliczyć długość łuku krzywej : a) y=lnx dla √3≤x≤√8 bardzo proszę o pomoc bo nie wiem jak to obliczyć . znam wzór na długość łuku ale po podstawieniu wychodzi całka której nie umiem ruszyć.

Trivial:

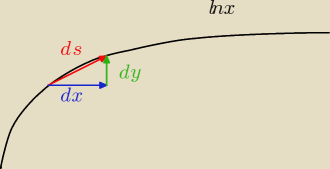
	dy
(ds)2 = (dx)2 + (dy)2 = (1 + (		)2)(dx)2
	dx

	x2+1
ds = √1 + (dy/dx)2dx = √1 + [(lnx)']2dx = √1 + 1/x2dx = √		dx =x>0=
	x2

	√x2+1
=		dx.
	x

Podstaw x = tgu i gotowe.

Trivial: Zadziała też magiczne podstawienie Eulera: √x²+1 = u − x.

Basia: f(x) = lnx x>0

	1
f'(x) =
	x

L = _√3∫^√8 √1+¹_x² dx

	√x2+1
J=∫√1+1x2 dx = ∫√x2+1x2 dx = ∫		dx
	x

t = √x²+1 t² = x²+1 x² = t²−1 x = √t²−1

	1
dt =		*2x dx
	2√x2+1

	x
dt =		dx
	√x2+1

	√x2+1		t
dx =		dt =		dt
	x		√t2−1

	t		t		t2
J = ∫		*		dt = ∫		dt =
	√t2−1		√t2−1		t2−1

	t2−1+1		1
∫		dt = ∫1 dt + ∫		dt
	t2−1		t2−1

z tym już sobie na pewno poradzisz nie trzeba potem wracać do x, ale nie zapomnij o zmianie granic całkowania t₁ = √3+1 = 2 t₂ = √8+1 = 3

głupol: a co to jest u albo tgu?

głupol: Basi sposób bardziej odpowiada temu co miałem na uczelni . Dziękuje wam bardzo juz rozumiem

głupol: Basia a dlaczego akurat w taki sposób trzeba zmienic granice całkowania?

głupol: juz wymyślilem dlaczego ale czy na pewno jeśli zmieni sie granice całkowania to nie trzeba juz podstawiac x znow za t? wychodzi ten sam wynik?