geom.analityczna
Kasiaula: 1.Czy w czworokąt o wierzchołkach: A=(−3, 2), B=(4, 2), C=(2,5), D=(−1,5) można wpisać okrąg?
Odpowiedź uzasadnij. Napisz równanie okręgu opisanego na tym czworokącie.
12 maj 13:53
qjon:
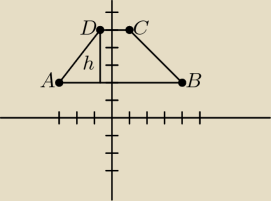
No to tak, aby sprawdzić czy w czworokąt można wpisać okrąg należy skorzystać z własności
czworokąta opisanego na okręgu, czyli:
|AB| + |CD| = |AD| + |BC|
no to liczymy
|AB| =
√ (4+3)2 + (2−2)2 =
√ 49 = 7
|CD| =
√ (2+1)2 + (5−5)2 =
√ 9 = 3
|AD| =
√ (−1+3)2 + (5−2)2 =
√ 4 + 9 =
√ 13
|BC| =
√ (2−4)2 + (5−2)2 =
√ 13
więc jak widać
|AB| + |CD| ≠ |AD| + |BC|, czyli w ten czworokąt okręgu nie wpiszemy.
Jako, że muszę wychodzić, to drugą część zrobię później jeśli ktos mnie nie uprzedzi

12 maj 14:22
Kasiaula: Dzięki

12 maj 14:36
 No to tak, aby sprawdzić czy w czworokąt można wpisać okrąg należy skorzystać z własności
czworokąta opisanego na okręgu, czyli:
|AB| + |CD| = |AD| + |BC|
no to liczymy
|AB| = √ (4+3)2 + (2−2)2 = √ 49 = 7
|CD| = √ (2+1)2 + (5−5)2 = √ 9 = 3
|AD| = √ (−1+3)2 + (5−2)2 = √ 4 + 9 = √ 13
|BC| = √ (2−4)2 + (5−2)2 = √ 13
więc jak widać
|AB| + |CD| ≠ |AD| + |BC|, czyli w ten czworokąt okręgu nie wpiszemy.
Jako, że muszę wychodzić, to drugą część zrobię później jeśli ktos mnie nie uprzedzi
No to tak, aby sprawdzić czy w czworokąt można wpisać okrąg należy skorzystać z własności
czworokąta opisanego na okręgu, czyli:
|AB| + |CD| = |AD| + |BC|
no to liczymy
|AB| = √ (4+3)2 + (2−2)2 = √ 49 = 7
|CD| = √ (2+1)2 + (5−5)2 = √ 9 = 3
|AD| = √ (−1+3)2 + (5−2)2 = √ 4 + 9 = √ 13
|BC| = √ (2−4)2 + (5−2)2 = √ 13
więc jak widać
|AB| + |CD| ≠ |AD| + |BC|, czyli w ten czworokąt okręgu nie wpiszemy.
Jako, że muszę wychodzić, to drugą część zrobię później jeśli ktos mnie nie uprzedzi 
