pole trapezu
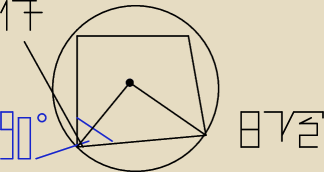
słaba z matematyki: Na okręgu opisano trapez prostokątny. Odległości środka okręgu od końców dłuższej
podstawy wynoszą i . Oblicz pole tego trapezu.
282 i 2/15 ma wyjść

24 kwi 17:17
proszę o pomoc: proszę o pomoc
24 kwi 18:07
proszę o pomoc: ja też mam problem z tym zadaniem
24 kwi 18:07
tim: brakuje dwóch liczb?

24 kwi 18:08
24 kwi 18:13
proszę o pomoc: 8 pierwiastków z 2 i 17 cm
24 kwi 18:21
proszę o pomoc: Heej, jest ktoś?
24 kwi 18:28
anka:
24 kwi 18:34
tim: Aniu może ja zrobię..? Mogę?
24 kwi 18:37
anka: może wiesz timusiu gdzie poszedłxpt .. bo miał mi pomóc przy zadaniu

a go nie ma ,
może go zastąpisz , to zadanie też możesz zrobić , ja chciałam sobie porysować

24 kwi 18:38
tim:
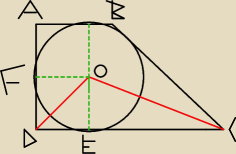
|DO| = 8
√2
|DO| jest przekątną kwadratu FOED o boku r, więc r
√2 = 8
√2, r = 8

|AD| = 16
|OC| = 17, |OE| = 8
Z tw. Pitagorasa |OE|
2 + |EC|
2 = |OC|
2, więc |EC| = 15
|EC| = 15
|DC| = 23
24 kwi 18:42
proszę o pomoc: a AB?
24 kwi 18:44
tim: Zaraz spróbuję dojść

24 kwi 18:45
anka: teraz jescze mi zadanie wytłumacz .. to z ośmiokątem

24 kwi 18:45
tim: Z ośmiokątem to xpt

only

24 kwi 18:49
anka: ja myślałam że ty też umiesz .. ale trochę nie zrozumiałam jego ironji .. ''chyba że tim
cośtam cośtam ... '' ?

24 kwi 18:55
anka: ironii**
24 kwi 18:57
proszę o pomoc: Co z tym \AB\ ? ? ?
24 kwi 19:08
anka: Czyżby tim zasnął a , może rozwiązuje ośmiokąta

24 kwi 19:13
proszę o pomoc: a może ty wiesz?
24 kwi 19:17
anka: nie ,, pochłonięta estm moim ośmiokątem

niestety nie mogę Ci pomóc , ale z pewnością
timuś zaraz tu będzie

24 kwi 19:21
tim: Już.. AB

24 kwi 19:30
24 kwi 19:30
tim:
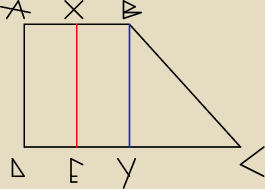
Rozwiązanie może trochę zawiłe, ale chyba jedyne

Szukamy |AB|.
Znamy
|AD| = |BY| = 16
|DC| = 23
|DE| = |AX| = 8
|EC| = 15
|EY| = |XB| = x
|BC| = y
Mamy dwie zależności
|BY|
2 + |YC|
2 = |BC|
2
Oraz czworokąt opisany na kole
|AD| + |BC| = |AB| + |DC|
Podstawiasz to co masz i masz równanie z dwoma niewiadomymi

24 kwi 19:33
tim: Tzn Eta jeżeli masz inny sposób to mów

24 kwi 19:33
Eta: Witam

Timuś sposób taki jak Twój

wprowadzimy prostsze oznaczenia:
IDCI=a I ABI = b IBCI = l IYCI = a − b => IYCI = 23 − b
z w−ku opisania trapezu mamy:
a +b = 2r +l
23 +b = 16 +l => l = b +7
teraz tak jak napisałeś z tw. Pitagorasa:
l
2 = (2r)
2 + IYCI
2
( b+7)
2 = 16
2 + ( 23− b)
2
po podniesieniu do kwadratu i redukcji otrzymamy:
80b = 736 =>
b = 12415
wiec P=
a+b2*2r
po podstawieniu ....... P= 282
215 [j
2]
24 kwi 19:54
tim: No

, a już zwątpiłem w siebie

24 kwi 19:55
Eta: Nieeeeeee

Tim

24 kwi 20:00
Eta: Tim

... łatwiej jest wprowadzać oznaczenia jedno literowe

bardziej przejrzyste jest rozwiązanie, ok?
24 kwi 20:02
tim: Tak jest pani kapitan

24 kwi 20:08
Bogdan:
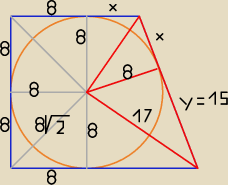
Z wzoru Pitagorasa obliczamy y =
√172 − 82 = 15.
| | x | | 8 | |
Czerwone trójkąty są podobne, więc zachodzi proporcja: |
| = |
| |
| | 8 | | 15 | |
| | 1 | | 64 | | 1 | | 2 | |
Pole trapezu P = 16*8 + 2* |
| *8* |
| + 2* |
| *8*15 = 282 |
| |
| | 2 | | 15 | | 2 | | 15 | |
24 kwi 20:11
Eta: 
24 kwi 20:12
tim: Ten to zawsze znajdzie prostsze rozwiązanie

24 kwi 20:13
24 kwi 20:13
Bogdan:

24 kwi 20:28
proszę o pomoc: Dzięki wszystkim, życie mi ratujecie już po raz kolejny

24 kwi 21:31
proszę o pomoc: Ah, Bogdan, jeszcze pytanko, jak Ty obliczyłeś to pole trapezu? Bo jakoś nie czaję skąd
ta 16
24 kwi 21:35
Bogdan:
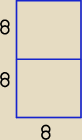
Lewa strona trapezu to prostokąt o wymiarach 16 na 8
24 kwi 21:46
proszę o pomoc: Ahia, a możesz wytłumaczyć resztę ze wzoru na pole?
24 kwi 21:52
proszę o pomoc: A nie, już czaję, 2 x pole trójkąta..
24 kwi 21:55
xpt: proszę o pomoc: masz 2 takie trójkąty (co widać na rysunku) mają dokładnie te same
wymiary, więc wzór na pole mają również taki sam.
anka: to z timem to było do tima, bo mnie zawsze wyprzedza z odpowiedzią ;)
24 kwi 22:00








 a go nie ma ,
może go zastąpisz , to zadanie też możesz zrobić , ja chciałam sobie porysować
a go nie ma ,
może go zastąpisz , to zadanie też możesz zrobić , ja chciałam sobie porysować 
 |DO| = 8√2
|DO| jest przekątną kwadratu FOED o boku r, więc r√2 = 8√2, r = 8
|DO| = 8√2
|DO| jest przekątną kwadratu FOED o boku r, więc r√2 = 8√2, r = 8  |AD| = 16
|OC| = 17, |OE| = 8
Z tw. Pitagorasa |OE|2 + |EC|2 = |OC|2, więc |EC| = 15
|EC| = 15
|DC| = 23
|AD| = 16
|OC| = 17, |OE| = 8
Z tw. Pitagorasa |OE|2 + |EC|2 = |OC|2, więc |EC| = 15
|EC| = 15
|DC| = 23


 only
only 


 niestety nie mogę Ci pomóc , ale z pewnością
timuś zaraz tu będzie
niestety nie mogę Ci pomóc , ale z pewnością
timuś zaraz tu będzie 




 jesteś?
bo ja mogę podpowiedzieć? .... jak wyliczyć "b"
jesteś?
bo ja mogę podpowiedzieć? .... jak wyliczyć "b"
 Rozwiązanie może trochę zawiłe, ale chyba jedyne
Rozwiązanie może trochę zawiłe, ale chyba jedyne  Szukamy |AB|.
Znamy
|AD| = |BY| = 16
|DC| = 23
|DE| = |AX| = 8
|EC| = 15
|EY| = |XB| = x
|BC| = y
Mamy dwie zależności
|BY|2 + |YC|2 = |BC|2
Oraz czworokąt opisany na kole
|AD| + |BC| = |AB| + |DC|
Podstawiasz to co masz i masz równanie z dwoma niewiadomymi
Szukamy |AB|.
Znamy
|AD| = |BY| = 16
|DC| = 23
|DE| = |AX| = 8
|EC| = 15
|EY| = |XB| = x
|BC| = y
Mamy dwie zależności
|BY|2 + |YC|2 = |BC|2
Oraz czworokąt opisany na kole
|AD| + |BC| = |AB| + |DC|
Podstawiasz to co masz i masz równanie z dwoma niewiadomymi 

 Timuś sposób taki jak Twój
Timuś sposób taki jak Twój  wprowadzimy prostsze oznaczenia:
IDCI=a I ABI = b IBCI = l IYCI = a − b => IYCI = 23 − b
z w−ku opisania trapezu mamy:
a +b = 2r +l
23 +b = 16 +l => l = b +7
teraz tak jak napisałeś z tw. Pitagorasa:
l2 = (2r)2 + IYCI2
( b+7)2 = 162 + ( 23− b)2
po podniesieniu do kwadratu i redukcji otrzymamy:
80b = 736 => b = 12415
wiec P= a+b2*2r
po podstawieniu ....... P= 282215 [j2]
wprowadzimy prostsze oznaczenia:
IDCI=a I ABI = b IBCI = l IYCI = a − b => IYCI = 23 − b
z w−ku opisania trapezu mamy:
a +b = 2r +l
23 +b = 16 +l => l = b +7
teraz tak jak napisałeś z tw. Pitagorasa:
l2 = (2r)2 + IYCI2
( b+7)2 = 162 + ( 23− b)2
po podniesieniu do kwadratu i redukcji otrzymamy:
80b = 736 => b = 12415
wiec P= a+b2*2r
po podstawieniu ....... P= 282215 [j2]
 , a już zwątpiłem w siebie
, a już zwątpiłem w siebie 
 Tim
Tim
 ... łatwiej jest wprowadzać oznaczenia jedno literowe
... łatwiej jest wprowadzać oznaczenia jedno literowe bardziej przejrzyste jest rozwiązanie, ok?
bardziej przejrzyste jest rozwiązanie, ok?

 Z wzoru Pitagorasa obliczamy y = √172 − 82 = 15.
Z wzoru Pitagorasa obliczamy y = √172 − 82 = 15.







 Lewa strona trapezu to prostokąt o wymiarach 16 na 8
Lewa strona trapezu to prostokąt o wymiarach 16 na 8