Zadanie Janek: I need help ! Zad. W trójkącie równoramiennym ABC, w którym IACI=IBCI i IABI= 10 poprowadzono dwusieczną kąta BAC, przecinającą bok BC w punkcie D. Wówczas okazało się,że IADI=IABI=ICDI. a) Wyznacz miary kątów trójkąta ABC b) Oblicz długość ramienia AC.

tim: To zadanie jest nieśmiertelne Już pomagam.

Janek: Niesmiertelne Te zadania są dziwne szczególnie dla humanistów

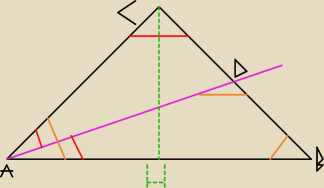tim: |AC| = |BC| więc kąty |BAC| oraz |ABC| są równe (pomarańczowy kolor α ). |AD| = |AB| więc bok |AD| = 10 i kąty |ADB| oraz |DBA| są równe (również α)

	1
Także |AD| = |DC| = 10, więc i kąty |CAD| oraz |DCA| są równe (		α)
	2

	1
Wracamy do trójkąta |ABC|. Składa się on z kątów |ACB| =		α, |CAB| = α oraz |CBA| =
	2

α. 2,5a = 180 a = 72 Więc kąty ||CBA| oraz |CAB| = 72, a kąt |ACB| = 36 AC policzysz prowadząc zieloną wysokość i korzystając z cosinusa kąta |CAB|, gdyż |AH| = 5

tim: Tak nieśmiertelne, bo za każdym razem się pojawiają, czy to na maturze, czy na sprawdzianie, czy nawet na forum tylko w innych formach