pole dwunastokąta anka : Jakie pole ma dwunastokąt foremny wpisany w okrąg o promieniu długości 5 ?

tim: W moich magicznych tablicach jest wzór, ale poczekam na twórcze rozwiązanie np. Bogdana czy Ety

anka : mój korepetytor dzisiaj się z tym męczył , dodam że nie rozwiązał

tim: To jakiś słaby [bez obrazy]

anka : ja jestem z 2 gim . i nie chciał mi trygonometrią w głowie mącić .

tim: A to co innego To witam, ja również

anka : witam miło mi ale przez nigo mam teraz problem bo sądze że jak pani zada takie zad. na spr. który ma być w poniedziałek to będzie nie ciekawie

tim: Ja podam propozycję rozwiązania:

	a√2(√3+1)
R koła opisanego na dwunastokącie = R =
	2

Wyliczamy z tego a = 5(√6 − √2) Podstawiamy do wzoru na Pole dwunastokąta foremnego P= 3a²(2 + √3) i wyliczamy.

tim: a = 2,5(√6 − √2) *

anka : o no wyszło (korepetytorowi) mu coś w stylu 2,5 xD

Bogdan: Jeśli wielokąt foremny o n bokach wpisany jest w okrąg o promieniu R, to

	1		360o
pole tego wielokąta P = n*		R2sin		.
	2		n

W tym przypadku n = 12, R = 5

	1		1
P = 12 *		* 52 * sin30o = 6 * 25 *		= 75
	2		2

anka : no ale , ja jescze nie wiem co to są te sin .. ( teoretycznie) bo jescze takiego czegoś nie mieliśmy

Bogdan: A to przepraszam, nie zauważyłem, że nie jesteś z gimnazjum.

sysia : jestem z gimn . z 2

sysia : ona ** jest z gimnazjum z 2

tim: sysia wpadłas

sysia : jak jabłko w kompot ?

anka : ojoj !

xpt: Zadanie do zrobienia w sposób analogiczny do tego z ośmiokątem tylko, ze z wykorzystaniem trójkąta o kątach 30^o, 60^o, 90^o zamiast 45^o, 45^o, 90^o.

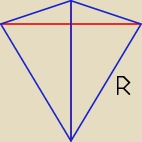
Bogdan: Dobry wieczór. Chciałem napisać, że nie jesteś z liceum, przejęzyczyłem się. Wróćmy do zadania i rozwiążemy je bez stosowania trygonometrii. 12−kąt foremny zbudowany jest z 6 deltoidów o przekątnych długości R, gdzie R to długość promienia okręgu opisanego na 12−kącie. R = 5.

	1
Pole 12−kąta P = 6 *		R2 = 3 * 25 = 75
	2

	1
Przypominam wzór na pole deltoidu o przekątnych d1, d2: P =		d1d2.
	2

W naszym zadaniu d₁ = d₂ = R = 5

anka: bogdan ? , a umiał byś tak ak xpt ? bo on to zrobił tymi kątami 30 60 90 .. , tyle że ja nie wiem z kąd ta wysokość tyle wynosi .. ( w moim 8 kącie)

anka: muszę się pochwalić zrobiłam 12 kąta metodą xpt i wyszło D

Bogdan: Można rozwiązywać zadania różnymi sposobami, ale przede wszystkim staramy się znaleźć rozwiązania najprostsze, najmniej czasochłonne (co jest ważne podczas sprawdzianów i egzaminów, gdzie musimy się zmieścić w określonym czasie), z jak najmniejszą liczbą przekształceń i obliczeń (im ich więcej, tym większe prawdopodobieństwo popełnienia błędu). Zachęcam do poszukiwania najprostszych rozwiązań zadań. Proste rozwiązania świadczą o tym, że matematyka w wydaniu szkolnym jest prosta i łatwa.