Rozwiąż nierówność Lena: a) π( x + π) ≥ √10 (x + √10) b)I√2 − xI ≥ 1 − √2

Maslanek: a) πx + π² ≥ x√10 + 10 x(π−√10 ≥ 10 − π²

	10−π2
x ≤		−−> Zmiana znaku, bo √10>π.
	π−√10

b) Prawa strona jest mniejsza od zera. Natomiast lewa zawsze większa. Zatem x∊R.

Patronus: πx + π² ≥ x√10 + 10 x(π−√10) ≥ 10 − π² { π−√10 jest większe od zera }

	10 − π2
x ≥
	π − √10

Maslanek: Mniejsze drogi Patronusie.

Patronus: racja Maslanek − zamiast √10 myślałem o √3 − roztrzepaniec...

Nienor: xπ+π²≥p₁₀x+10 xπ−p₁₀x≥10−π² x(π−p₁₀)≥−(π²−10)

	π2−10
x≥
	p10−π

2. Całe R, bo 1−p₂ jest mniejsze od 0, natomiast lewa strona jest zawsze dodatnia.

Maslanek: Dużo jeszcze osób to zrobi i nie zmieni znaku?... Ja specjalnie na kalkulatorze sprawdzałem ile to jest

Nienor: touche

Lena: a taki przykład √π (√π − x)∠ √2 (x+ √2)

Maslanek:

Maslanek: Podobnie zapewne

Nienor: analogicznie do poprzednich spróbuj sama

Lena: już rozwiązałam a czy znak na koniec też zmieniam czy nie

Maslanek: Jeśli to coś w nawiasie jest ujemne to tak.

Lena:

	2 − π
wyszło mi x		taki jaki znak
	−√π − √2

Nienor: −√π−√2 jest liczbą ujemną, więc znak zmieniasz.

Lena: może ktoś ten przykład b rozpisać

ania: |cokolwiek| ≥ liczba ujemna spełnione zawsze

Lena: pomieszaliście mi a więc co będzie z tymi przykładami: a) Ix− 3I<−3 b)I6 − xI≥ −1

Nienor: a) Zbiór pusty b) całe R https://matematykaszkolna.pl/strona/15.html − własności wartości bezwzględnej.

Aga1.: a Ix−3I<−3 Nierówność sprzeczna, brak rozwiązania b) I6−xI≥−1 odp. x∊R.( bo IxI≥0, wartość bezwzględna dowolnej liczby rzeczywistej jest ≥0, to tym bardziej ≥ −1)

Lena: dobra kumam dzięki a w takim I1−xI ≥0

Maslanek: x∊R

Lena: a w takim przykładzie Ix−4I <0 x∊R − {4}

ania: w tym ostatnim zbiór pusty

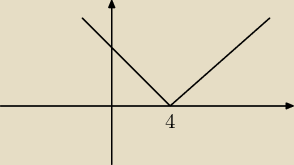
ania: to jest |x−4| jak widać nigdy nie jest mniejsze od zera

Nienor: dokładnie.

Lena: czy dobrze zrobiłam

Maslanek: x∊∅

Lena: a w takim przykładzie Ix−3I>0 x∊R − {3}

Maslanek: ta

Lena: Ix+2I ≤0 ? a tu jaki wynik?

Lena: tu będzie albo x jest pusty lub x ∊R

Lena:

ania: |x−2| <0 to zbiór pusty tak jak ma rysunku z 4 tylko zamiast 4 wstaw 2 ale tu masz jeszcze warynek ze |x−2| =0 a na rysunku widać że do zera dotyka w czubku więc odpowiedzią tutaj jest x=2

Lenba: Ix+2I ≤0 ale tu jest tak

ania: dlatego odp: x=2

Lena: a dlaczego nie x=−2

Nienor: Jedź z definicji

	⎧	x+2≤0,dla x+2≥0
Ix+2I ≤0=	⎩	−(x+2)≥0, dla x+2<0

ania: aa ok −2 no już kapujesz ;>

Lena: zrobiłam tak i nie co jest w tym złego x + 2 ≤0 x+2≥0 x≤−2 x≥−2

Lena: więc x∊R a coś mi wtedy nie pasuje nie wiem

Nienor: dodaj warunki, wtedy z pierwszego zostaje tylko x=−2, a w drugim wszystko odpada.

Lena: a mógłbyś to napisać bo nie kumam

Nienor: masz tam napisane dla x≥−2 w pierwszym i dla x<−2 w drugim, jak naniesiesz te przedziały na swoją odp. to ci wyjdzie dobrze. Wszystko co tu było pisane wynika właśnie z tego.