rysunek endzia1: Prosze o rysunek 2)Twierdzenie. Jeżeli n prostych zawiera się w jednej płaszczyźnie i żadne dwie nie są równoległe oraz żadne trzy nie przechodzą przez jeden punkt, to proste te rozcinają płaszczyznę na (n² + n + 2)/2 rozłącznych części. a) Oblicz, na ile rozłącznych części dzielą płaszczyznę cztery proste spełniające podane w twierdzeniu warunki. Wykonaj rysunek obrazujący ten podział b) Na płaszczyźnie leży k prostych spełniających podane w twierdzeniu warunki. O ile zmniejszy się liczba części, na które dzielą płaszczyznę proste, jeżeli usuniemy jedną z tych prostych ?

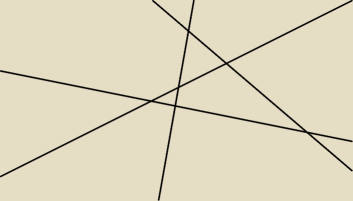
panteon: 11 części zgodnie ze wzorem

panteon: b.)^{n2 + n + 2}₂ − ^{(n−1)2 +n − 1 + 2}₂