PRAWDOPODOBIEŃSTWO ZADANIE 11 Yay: słuchajcie mam prosbę tylko jednego zadanie nie zrobiłem i nie wiem jak je zrobić zadanie ostatnie z prawdopodobieństwem. Niby logiczne ale nie mogłem znaleść dowodu przekonywujacego mnie. Pomoże ktoś?

Aranea: Zrób sobie rysunek.P(A`∩B) = P(B) − P(A∩B). Po drugie P(B`∩A) = P(A) − P(A∩B). Po trzecie 1≥P(A) + P(B) − P(A∩B). Czyli 1 ≥ P(A) + 0,7. 0,3 ≥ P(A), a wiadomo, że P(A) ≥ P(A) − P(A∩B). Stąd P(B`∩A)≥0,3

Basia: proponuję tak: A'∩B = (A∪B')' ⇒ 0,7 = P[(A∪B')'] = 1−P(A∪B') ⇒ P(A∪B') = 0,3 B'∩A = A∩B' ⊂ A∪B' ⇒ P(B'∩A) ≤ P(A∪B') = 0,3 c.b.d.o.

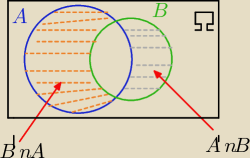
Eta: 3/ sposób Zdarzenia (B^'∩A) i (A^'∩B) −−− są rozłączne ( nie mają części wspólnej) zatem: P(A∩B^') +P(A^'∩B) ≤ 1 to 0,7+P(A^'∩B)≤1 ⇒ P(A^'∩B) ≤ 1−0,7 ⇒ P(A^'∩B)≤0,3 c.n.u.