. elpe: Rozszerzenie 2012 Jak Wam poszlo i jak oceniacie. Osobiście napisałem na ok. 60−80% i wydawała sie trudniejsza niż zeszłoroczna

aaa: Mi sie wydaje ze mam ok. 85/90 % oczywiscie jak zawsze zjebalem prawdopodobieństwo. xd

elpe: w sumie to nie była taka zła jak ktoś sie uczył 9 kijowe ale no nic nie ma co zapeszać

hh: ile wam wyszlo to z tymi liczbami? ile ich jest

Pati: bedzie cos kolo 90 glupie bledy znowu

TOmek: 952

Pati: hh 280

ttt: 20...

Kaka: Ja pitole same koksy są na tej stronie ,trudna była wg mnie i pewnie bede mial max 40%

Error_Demon: Mnie ciężko ocenić niby zrobiłem 8/11 zadań do końca więc jeśli gdzieś się nie pomyliłem to w porządku a w pozostałych trzech liczę na jakieś punkty bo coś tam robiłem ale nie mogłem dojść do rozwiązania. Mam nadzieję że te rozwiązane są rozwiązana dobrze.

Daniel: POZDRO− ZEMDLAŁEM / moge sie juz pozegnac ze studiami, chyba ze w piatek fiza rozsz na 100%

TOmek: ile wam wyszlo z tym prostokątem?

	ab3
P=
	2(a2+b2)

rumpek:

TOmek: zajebiscie

TOmek: a liczb 8 cyfrowych to 952

Error_Demon: Też chyba miałem 952

jarke: pamięta ktoś treść tego zadania z parametrem z analitycznej?

TOmek: to było banalne wyszło

	2605		2045
najmniejsza		i najwieksza		tak?
	4		4

Adam: Mi największa wyszła ²⁶⁰⁵₄ a najmniejsza chyba 500

TOmek:

	3+√37
W parametrze mi wyszło m=√		co nie nalezlo do rozwiązania "Δ>0"
	2

Error_Demon: Najmniejsza 500, największa ²⁰⁴⁵₄

Error_Demon: Tomek jak najmniejsza mogła Ci wyjść większa od największej?

luc: ja się zamotałem w 3 warunku x₁⁴+x₂⁴ rozpisałem to ze wzorów skróconego, moze ktos to rozpisać dla mnie?

TOmek: zle przepisalem, powinno byc na odwrot

	2045
najmniejsza −>		blabla
	4

TOmek: (x₁²)²+(x₂²)²=(x₁²+x₂²)²−2(x₁x₂)² teraz rozpisze :x₁²+x₂²=(x₁+x₂)²−2x₁*x₂ zatem((x₁+x₂)²−2x₁*x₂)²−2(x₁x₂)²

kylo1303: rumpek Jak poszlo? Jesli chodzi o wartosci najwieksza i najmniejsza to mam inaczej bo mi liczby calkowite wychodzily. I wartosci te byly na granicach przedzialu <−1,7>.

rumpek: Nie obstawiam wyniku chociaż widzę niektóre podobne zadanie z parametrem m = −√14 v m = √14 W sumie od 80% będę zadowolony

luc: tak miałem i podstawilem m i skomplikowane równanie wyszło 4 stopnia chyba?

luc: tez ci takie wyszło tomek?

TOmek: równanie 4 stopnia wyszło, tylko mi cos pierwiastki nie te wyszly

luc: to mam dobrze do tego miejsca wiec pewnie nie bedzie za czesc wspólna i odp pktów?

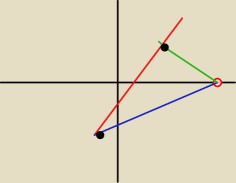
Error_Demon: TOmek dlaczego tak nie było przypadkiem że dla m=−1 jest największa, a najmniejsza kiedy m należało do prostej prostopadłej i przechodzącej przez Q?

Pepsi2092: Ja osobiście liczę na 70−80% także nie ma tragedii napiszcie mi jak zadanie z tym |PQ| liczyliście, bo ja to zrobiłem z odległosci dwóch pktów P i Q i wyszła mi funkcja kwadratowa, sprawdziłem czy wierzchołek należy do przedziału, nie należał więc policzyłem wartości dla skrajnych liczb z dziedziny ale słucham Was

TOmek: robiłem tak jak Pepsi napisał

luc: jak sie nie napisało tego warunku w PQ z funkcja kwadratowa tylko przedziały od razu policzyło to odejma pkt? jak myślicie?

psik: robiłem tak jak Tomek napisał ale spieprzyłem . Bo porównywałem współczynniki wielomianów zamiast przenosić na drugą stronę D:

Bartek0807: osobiście nie jestem pewny kombinatoryki i nie zrobiłem ostatniego bo nie miałem pomysłu a tak to wszystko

max: Ostatnie było łatwe.. P(A'∩B)≥0,7 z tego wynika, że P(A') musi być na pewno ≥0,7 wynika to z części wspólnej. Skoro P(A')≥0,7 to P(A)≤0,3. No i znów z części wspólnej P(A∩B') na pewno jest mniejsze bądź równe 0,3 bo P(A)≤0,3. Ja poległem na tej odległości punktów...

max: A kombinatoryka 12=2*2*3 12=3*4 i 12=6*2 i na 3 przypadki. W pierwszym 8 po 2 razy 6 czyli 28*6 możliwości W drugim 8*7 możliwości W trzecim 8*7 możliwości Razem tam wyszło chyba 260 albo 280 jeśli dobrze pamiętam