zadanko tosia: 1.Dany jest okrąg o równaniu (x−5)²+(y+1)²=25.Długość tego okręgu jest równa 2.Największą wartością funkcji kwadratowej (f)=−2(x+3)²−4 jest? 3.Zbiorem rozwiązań nierówności (x−2)(x+5)większe lub równe od zera proszę o wyjaśnienie podanych zagadnień w sposób zrozumiały z góry dziękuję

Patronus: 1. promień to √25 = 5 długość okręgu to inaczej obwód czyli 2πr= 10π 2. policz wierzchołek W = (x_w, y_w), y_w to największa wartość funkcji

Sławek.: 10π −4 (−∞,−5>u<2,+∞)

ania: 1. długość okręgu to 2πr ze wzoru widać że r=5 więc długość to 10π 2. max to wierzchołek czyli (−3;−4) więc największa wartość to −4 3. x≤−5 u x≥2

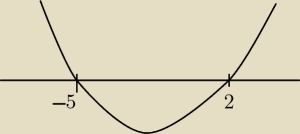
Patronus: 3) miejsca zerowe to −5 i 2, funkcja ma współczynnik przy x² dodatni czyli ramiona skierowane do góry, rysujesz poglądowy wykres i patrzysz w jakim przedziale funkcja jest mniejsz lub równa 0 Ano w takim x∊<−5;2>

picia: ma byc wieksze lub rowne 0

Aga1.: Odp. do zad. 3. (x−2)(x+5)≥0⇔x∊(−∞,−5>U <2,∞)

tosia: W ciągu geometrycznym drugi wyraz jest równy (−2) , a trzeci wyraz (−18). Iloraz tego ciągu jest równy? jakich tu wzorów należy użyć?

ania: q=−18/−2 = 9

Sławek.: a2 * q = a3 −2 * q = −18

	−18
q =
	−2

q = 9