Trygonometria - odległość wierzchołka od przekątnej Kamila: W prostokącie ABCD przekątne mają długość 16 cm i przecinają się pod kątem 50 stopni. Oblicz odległość wierzchołka A od przekątnej BD z dokładnością do 0,01cm. Po pierwsze: jak to rozwiązać? Po drugie (ale to już mniej ważne): dlaczego rozwiązaniem nie jest poprostu 8cm, bo nie rozumiem tego Z góry dzięki za odpowiedzi

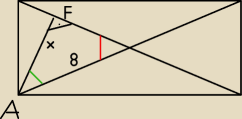xpt: Odleglosc od przekatnej to dlugosc |AF|=x Ponieważ odległośc punktu od prostej to długośc odcinka, lezącego pod kątem prostym do prostej z końcami na prostej i w punkcie A. na czerwono zaznaczono kąt 50^o na zielono kąt 40^o

	8		x
Z funkcji trygonometrycznych oblicz		bądź		, z tablic odczytaj przybliżoną
	x		8

watrość funkcji i zaokrąglij do 0,01 cm ;)

Kamila: Dzięki wielkie Nie zrozumiałam czego dokładnie ode mnie chcą z tą odległością Dziękuję jeszcze raz i pozdrawiam

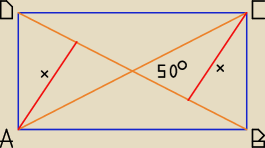Bogdan: Jeśli w czworokącie wypukłym dane są długości przekątnych d₁, d₂ oraz miara kąta α

	1
między nimi, to pole P tego czworokąta wyraża się wzorem: P =		d1d2sinα.
	2

	1
W tym zadaniu d1 = d2 = 16, a więc P =		* 162sin50o = 128sin50o.
	2

x − odległość wierzchołka A prostokąta od przekątnej BD oraz wierzchołka C od przekątnej BD

	1
Pole prostokąta P = 2 *		* 16 * x = 16x
	2

16x = 128sin50^o => x = 8sin50^o