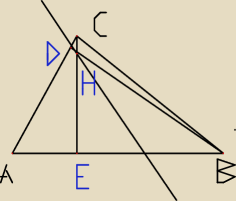
Wykaż, że prosta zawierająca dwusieczną kąta BHE przechodzi przez środek okręgu konrad: W trójkącie ostrokątnym ABC ∠BAC = 60°. Wysokości BD i CE tego trójkąta przecinają się w punkcie H. Wykaż, że prosta zawierająca dwusieczną kąta BHE przechodzi przez środek okręgu opisanego na trójkącie ABC.

Basia: Pomagam

Basia: ∠BAC = 60 ⇒ ∠ACE = 30 ⇒ ∠CHD = 60 ⇒ ∠EHB = 60 ⇒ ∠EBH = 30 ⇒ ∠BCA = 60 ⇒ ABC jest trójkątem równobocznym ⇒ H jest środkiem okręgu opisanego na ABC (bo w tr.równobocznym wysokości pokrywają się z symetralnymi) H ∈ dwusiecznej EHB

konrad: hmm... jak z faktu, że ∠EHB = 60 wywnioskowałaś, że ∠EBH = 30 ?

konrad: hm... jak wywnioskowałaś z ∠EHB = 60 , że ∠EBH = 30 ?

Basia: EC jest wysokością ⇒ tr.EHB jest prostokatny

Basia: Sorry ale tam jest błąd. Jeszcze pomyślę

konrad: Trzeba czegoś bardziej ogólnego, bo gdy to sobie narysujesz (tzn wyrysujesz środek tego koła) to wychodzi jakiś punkt na tej 2siecznej, który nie jest punktem H

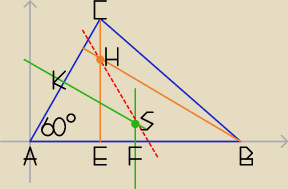
Bogdan: Można spróbować nałożyć na rysunek układ współrzędnych.

	b		e		√3e
A(0, 0), E(e, 0), F(		, 0), B(b, 0), K(		,		), C(e, √3e)
	2		2		2

Prosta AKC: y = √3x Prosta EC: x = e

	b
Prosta FS: x =
	2

	√3		2√3e
Prosta KS: y = −		x +
	3		3

Teraz można wyznaczyć równanie prostej BH, punkty H i S oraz równanie dwusiecznej HS i sprawdzić, czy S należy do dwusiecznej HS. Jest trochę liczenia. Może uda się znaleźć prostszy sposób. Czas spać. Dobranoc

Bogdan: Dodam, że prosta HS to prosta Eulera. http://pl.wikipedia.org/wiki/Prosta_Eulera

konrad: to wystarczałoby udowodnić, że prosta eulera jest dwusieczną kąta utworzonego przez wysokości