? ania: Nie wiem jak to zrobić − W trapezie prostokątnym o polu 24cm² i kącie ostrym 45 stopni dłuższa przekątna tworzy z podstawami kąt alfa , taki że tg = 1/2 . Oblicz obwód tego trapezu. i drugie zad W trapezie prostokątnym kąt DAB ma miarę 30 stopni, a boki AD i AB mają odpowiednio długości 10 cm i 14 cm . Oblicz pole tego trapezu . Bardzo prosze o pomoc . Ważna to sprawa.

ania: ktoś pomoże

tim: Spróbuję pomóc pierwsze.

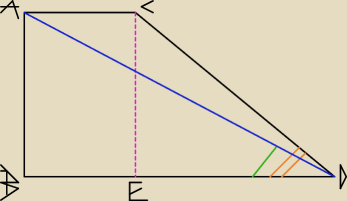tim: Kąt pomarańczowy = 45^O. Wynika z tego, że trójkąt CDE jest równoramienny oraz |CE| = |ED| = |AB| = h. Wynika z rysunku także, że |AC| = |BE| = a.

	1
Z tangensa wynika że stosunek |AB| do |BD| =		.
	2

Czyli |AB| = |CE| = |ED| = 1 * n Oraz |BD| = 2 * n |BE| = |BD| − |ED| = 1 * n

	(|AC| + |BD|) * |AB|
Wiemy, że		= 24
	2

(2n + 1n) * 1n
	= 24
2

3n² = 48 n² = 16 n = 4 Więc. |AC| = 1 * 4 = 4 |AB| = 1 * 4 = 4 |BD| = 2 * 4 = 8 |CD|² = |CE|² + |ED|² Z pitagorasa.. Dalej dodajesz i masz obwód.

ania: aha , dzięki

tim: Jeżeli czegoś nie rozumiesz to napisz

ania: a tego drugiego to nie trzeba ale za to mam problem z tym : trapez równoramienny o podstawach 5 cm i 3,2 cm opisany jest na okręgu o promieniu 2 cm . Oblicz pole i miary kątów tego trapezu. Oblicz pole trapezu równoramiennego , którego kąt ostry ma miare 30 stopni a podstawy mają dł 4 i 10 cm.

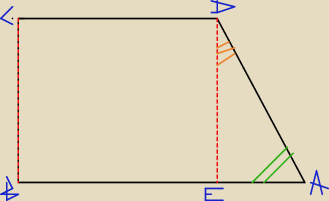tim: Ok. Następne. Kąty w trójkącie DEA to zielony 30 i pomarańczowy 60. Z funkcji trygonometrycznych obliczamy, skoro |DA| = 10 to |DE| = 5 oraz |EA| = 5√3. Skoro |AB| ma 14, to |BE| = |CD| = 14 − 5√3. Pole:

(a + b) * h
2

(14 + 14 − 5√3) * 5
2

(28 − 5√3) * 2,5 = 70 − 12,5√3

tim: Oh już za późno

ania: dziękuje

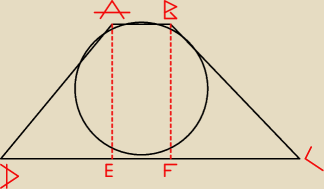tim: Ok. Teraz z kołem. |AB| = 3,2 |CD| = 5 |AE| = |BF| = 2r = 4

	5 − 3,2
|DE| =		= 0,9
	2

Liczysz tangens z kąta ADE, gdzie a = |AE|, a b = |DE|. Kąt ADE = BCF (jest równoramienny). Kąt DAB = CBA (jest równoramienny) = 180 − ADE Pole obliczysz sama

ania: o bardzo dziękuje

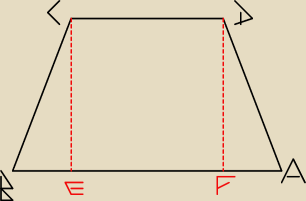tim: Jeszcze ostatnie. Najprostsze chyba |CD| = 4 |AB| = 10 |BE| = |FA| = 6/2 = 3 Kąty EBC oraz FAD są równe, mają 30^O.

	h		√3
Z tangensa z 30O obliczamy		=		h = √3
	BE		3

Pole potrafisz.

ania: dzięki za pomoc , pozdrawiam

tim: Za ew. pomyłki przepraszam

OLa: o co chodzi?