wzór Franek: wykres funkcji

	2
f(x)=1+
	x−3

narysuj f(|x|) czy mógł by mi ktoś narysować bo mi nie wychodzi

sazzi001:

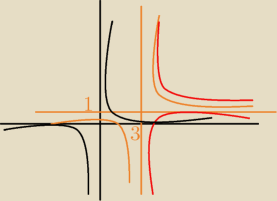
	2
na czarno		, na czerwono f(x) na niebiesko wartość bezwzgędna z samego x. wydaje mi się
	x

że dobrze

Franek: żle

Franek: http://www.wolframalpha.com/input/?i=domain+of+f%28x%29+%3D+1+%2B+2%2F%28%7Cx%7C-3%29 wytłumaczy mi ktoś czemu tej dolnej "paraboli" końce nie są przedłużone?

Franek: górne końce dolnej paraboli bo kończą się na osi OY

Franek:

Franek:

sazzi001: podbijam... nurtuje mnie to^^

sazzi001: podbijam... nurtuje mnie to^^

Kaśka: a gdzie tu parabola?! O.O

sazzi001: nie parabola tylko hiperbola. z tym że jest odbita w ten sposób, że sprawia wrażenie paraboli

Basiek: Nie rozumiem pytania. Ale już Ci mówię, jak to narysować.

	2
1) rysujesz
	x

2) przesuwasz o wektor [3,1] 3) nakładasz na argument moduł, więc wszystko, co masz po prawej przerysowywujesz symetrycznie na lewo!

Kaśka: mi to wychodzi zupełnie inaczej..

sazzi001: Basiek : na pewno w lewo? to już wiem co zorobiłam źle... po prostu odbiłam w drugą stronę

Basiek: Prawo na lewo. Tak, powtarzam to już na tym forum dosłownie 20x. Więc tak. Prawo na lewo.

Rafał274: Zasada prosta. Rysujemy wykres funkcji f(x) tylko dla przedziału <0; +∞) a następnie symetrycznie odbijamy względem osi OY całość po prawej stronie na lewą stronę i mamy wykres funkcji f(|x|)

Basiek: Dokładnie. Miało się to 3 z przekształceń funkcji Teraz się wszystko powinno pokrywać z wolframem

Franek: a czemu dla <0, +niesk)

Basiek: To wygląda tak, że gdybyś narysował sobie cały wykres dla od (−∞,+∞), to jak nakładasz moduł na argument, to odbijasz CAŁĄ PRAWĄ STRONĘ (więc od <0,+∞) ) na LEWO (która jest przecież czysta, nie ma....).

Saizou : @Basiek mogła byś zerknąć https://matematykaszkolna.pl/forum/145364.html

Franek: no tak ale końce tej dolnej nie przecinają się tylko są ucięte w OY

Basiek: Co? Oo

Franek: na tym wykresie to te hiperbole nie powinny się krzyżować i proste dalej "lecieć"?

Basiek: Na tym wykresie wszystko jest okej. Wyobraź sobie, że nie masz lewej strony. Cały ten wykres to zeszyt, oś OY to środek,pobaźgrałeś prawą stronę, zamknąłeś zeszyt i go otworzyłeś. Wszystko, co miałeś po prawo, masz teraz także jako odbicie lustrzane na lewo.

Franek: http://www.wolframalpha.com/input/?i=domain+of+f%28x%29+%3D+1+%2B+2%2F%28x-3%29 ta krzywa od (−niesk, 0) po lewej stronie czemu się na prawą nie odbija?

Basiek: Franek! Weź się w garść. W TYM PRZEKSZTAŁCENIU ODBIJAM PRAWO NA LEWO, NIC WIĘCEJ Twoje pytanie jest analogiczne do: Dlaczego, jak mam moduł na całej funkcji, to nie odbijam części, która leży powyżej OX ?

Franek: aha... a kiedy odbijamy w prawo tylko?

Basiek: Pytasz, kiedy odbijamy lewą stronę na prawą? Wtedy, gdy nakładamy pierwiastek Jednak kiepska ze mnie służąca

Franek: yy.. pierwiastek? może przykład?

Rafał274: Możemy odbijać albo z dołu na górę w przypadku gdy y = f(x) oraz y = |f(x)| oraz z prawej na lewą gdy y = f(x) i chcemy narysować y = f(|x|)

Basiek: Pierwiastka? Widziałam taki przykład w podręczniku Pazdro w pierwszej klasie. Od tego dużo zadań widziałam, ale kolejnego takiego przekształcenia to już nie , więc spokojnie. Jak wspominałam, ten temat ogarniam, bo miałam 3

Rafał274: A jeszcze odbijanie wykresów funkcji z lewej na prawą i na odwrót gdy y = f(x) oraz y = f(−x) oraz z góry na dół i odwrotnie, gdy y = f(x) i y = −f(x)

Franek: Basiek dziękuje ślicznie co ja bym bez Ciebie zrobił

Rafał274: Tutaj jest wszystko o odbijaniu. Pozdro. http://www.zadania.info/28578

Basiek: http://www.wolframalpha.com/input/?i=y%3Dx%2B2 http://www.wolframalpha.com/input/?i=y%3D%E2%88%9Ax+%2B2 Coś w ten deseń

Franek: Rafał274 dzięki Basiek

Basiek: Co byś zrobił? Poradziłbyś sobie Tymczasem znikam odpocząć od matematyki, będę wieczorem.