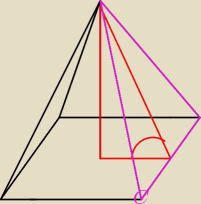
Stereometria Aniaaaaa: Dany jest ostrosłup prawidłowy czworokątny o podstawie ABCD i wierzchołku S. Ściana boczna jest nachylona do płaszczyzny podstawy pod kątem 60 stopni , zaś krawędź boczna jest równa 5. Oblicz objętość ostrosłupa. Widziałam odpowiedzi, ale robiąc innym sposobem, wyszedł mi inny wynik i nie wiem dlaczego nie mogę tak liczyć, albo gdzie popełniłam błąd. Krawędź boczna wynosi 5, a fioletowy jest równoramienny, czyli przy podstawie ma po 45 stopni, wiec z sin45 obliczyłam wysokość tego trójkąta oraz podstawę. Później korzystając z podanego kąta liczyłam z sin60 wysokość ostrosłupa, ale licząc dalej wynik wychodzi zupełnie inny.

Aniaaaaa: Czy ktoś pomoże

Mariola: spróbuję roztrzaskać....Najpierw pole podstawy a² czyli 5²=25. Obliczam teraz wysokość ostrosłupaPp=1/2a*h 25=1/2*5*h 25=5/2*h /: 5/2 25*2/5=h 10 =h I już mam wszystko, dane podstawiam pod wzór na objętość, czyli:V=1/3*Pp*h V=1/3*25*10 V=1/3*250 V≈8,3 PS. Tak mi wychodzi... trochę brzytki wynik, ale nie zawsze wychodzą ładne (mam nadzieję, że dobrze)