4 łatwe zadania Marlena: Mam 4 zadania. Potrzebuję samych wyników, ponieważ obliczyłem je. Nie wiem czy dobrze.Jeśli ktoś ma ochotę się rozpisywać to proszę Wezmę te obliczenia do rozpracowania przy błędnym wyniku, zobacze co pominąłem itp Jeśli komuś sie nudzi to może zrobić obliczenia, jednak prosiłbym aby były dosyć łatwe, nie z rozszerzonego; jakieś wzory o których na podstawie nie słyszano Oto one: 1) Pole podstawy stożka jest równe 27 π cm², a jego objętość równa 27π cm³. Wyznacz kąt między tworzącą stożka a jego podstawą .2) Przekątna przekroju osiowego walca jest nachylona do średnicy pod kątem 30 *. Oblicz Pc i V tego walca, wiedząc, że promień podstawy wynosi 8√3 . 3) Oblicz objętość kuli, wiedząc, że pole koła wielkiego wynosi 8π. 4) Przekrój osiowy stożka jest trójkątem równoramiennym o ramieniu a i kącie przy podstawie 60 *. Oblicz objętość i pole powierzchni tego stożka. Dziękuję z góry

Marlena: A w 4 nie mamy danego a ale jeśli sobie dobrze przypominam to wynik wyszedł z literkami a

Patronus: 3) P = 8π = πr² => r = √8 = 2√2

	4
V =		πr3 = ...
	3

Marlena: O 4 jakby ktoś mógł rozpisać dziwne wyniki wychodzą nawet po Pitagorasie. h=2 masakra

Marlena:

	2
Masakra wyszło mi w 4 zadaniu, że P= a2 a V=		πa
	3

sazzi001:

	a3√3π
4) V=
	24

	3a2π
Pc=
	4

Marlena: A jak zrobiłeś to 4? Mógłbyś rozpisać Ew rysunek poglądowy. Wyszło mi że Δ jest równoboczny.

Marlena: A jak zrobiłeś to 4? Mógłbyś rozpisać Ew rysunek poglądowy. Wyszło mi że Δ jest równoboczny.

sazzi001:

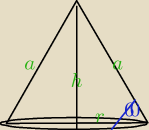
	1		r
cos60=		=
	2		a

	a
a=2r⇒r=
	2

	√3		h
sin60=		=
	2		a

a√3=2h

	a√3
h=
	2

	a3√3π
V=1/3π*a2/4*a√3/2=
	24

	3a2π
Pc=πa/2(a/2+a)=πa/2(3a/2)=
	4

Marlena: Dziękuje