Ile jest liczb naturalnych trzycyfrowych , w ktorych kazda cyfra jest inna i cy
Maciek: Ile jest liczb naturalnych trzycyfrowych , w ktorych kazda cyfra jest inna i cyfra jednosci
jest 5 ?
7 maj 12:33
Anivlam:
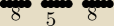
liczba trzycyfrowa, po srodku musi byc 5 (bo jest to miejsce jednosci) na pierwszym miejscu
jest 8 mozliwosci bo wybieramy sposrod 10 cyfr (0,1,2,3,4,5,6,7,8,9) jak wiadomo 0 nie moze
byc na pierwszym miejscu wiec automatycznie zostaje nam 9 mozliwosci, czyli 9 mozliwosci−1
mozliwosc(bo jedna cyfra juz jest wykorzystana w miejscu jednosci). Zajmijmy sie teraz trzecim
miejscem: zostaje nam rowniez 8 mozliwosci bo wybieramy sposrod 10 cyfr a odejmujemy dwie
mozliwosci ktore zostaly wczesniej wykorzystane. No i teraz z reguły mnożenia liczymy: 8x5x8
<− i to nasz wynik
7 maj 12:46
Maciek: ku ścisłości 5 to jest jedna liczba czyli zastępujemy 1 i wynik wychodzi prawidłowy
7 maj 20:23
Maciek: ku ścisłości 5 to jest jedna liczba czyli zastępujemy 1 i wynik wychodzi prawidłowy
7 maj 20:24
Maciek: To pierwsze jest co? nie powinno być najpierw − setki , dziesiątki , jedności?
7 maj 20:25
Saizou : a więc
− na pierwszym miejscu mogą być cyfry 1,2,3,4,6,7,8,9 co daje nam 8 możliwości
−na drugim mogą być 0,1,2,3,4,6,7,8,9 tylko pamiętaj że nie ta sama co na pierwszym więc 8
możliwości
−na 3 miejscu jest liczba 5 więc tylko 1 możliwość
8*8*1=64
7 maj 20:29
Saizou : tak mnie się wydaje
7 maj 20:29
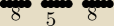 liczba trzycyfrowa, po srodku musi byc 5 (bo jest to miejsce jednosci) na pierwszym miejscu
jest 8 mozliwosci bo wybieramy sposrod 10 cyfr (0,1,2,3,4,5,6,7,8,9) jak wiadomo 0 nie moze
byc na pierwszym miejscu wiec automatycznie zostaje nam 9 mozliwosci, czyli 9 mozliwosci−1
mozliwosc(bo jedna cyfra juz jest wykorzystana w miejscu jednosci). Zajmijmy sie teraz trzecim
miejscem: zostaje nam rowniez 8 mozliwosci bo wybieramy sposrod 10 cyfr a odejmujemy dwie
mozliwosci ktore zostaly wczesniej wykorzystane. No i teraz z reguły mnożenia liczymy: 8x5x8
<− i to nasz wynik
liczba trzycyfrowa, po srodku musi byc 5 (bo jest to miejsce jednosci) na pierwszym miejscu
jest 8 mozliwosci bo wybieramy sposrod 10 cyfr (0,1,2,3,4,5,6,7,8,9) jak wiadomo 0 nie moze
byc na pierwszym miejscu wiec automatycznie zostaje nam 9 mozliwosci, czyli 9 mozliwosci−1
mozliwosc(bo jedna cyfra juz jest wykorzystana w miejscu jednosci). Zajmijmy sie teraz trzecim
miejscem: zostaje nam rowniez 8 mozliwosci bo wybieramy sposrod 10 cyfr a odejmujemy dwie
mozliwosci ktore zostaly wczesniej wykorzystane. No i teraz z reguły mnożenia liczymy: 8x5x8
<− i to nasz wynik